Hasta ahora se han estudiado los empréstitos enfocados desde el punto de vista del emisor, considerando la operación como un todo, centrándonos en la construcción de los cuadros de amortización.
Sin embargo, el obligacionista se plantea la necesidad de estimar la duración de los títulos que adquiere y la rentabilidad que le supondrán.
El estudio de la probabilidad en los empréstitos tiene razón de ser al considerar esta operación desde el punto de vista del obligacionista, el cual, cuando adquiere títulos desea conocer la rentabilidad de la inversión efectuada. Ahora bien, la rentabilidad efectiva implica conocer no sólo el importe económico de los derechos futuros (cupones, valor de reembolso y posibles lotes) sino del número de ellos, que, a su vez, dependerá del momento en el que el título resultará amortizado.
Dado que la amortización de los títulos se realiza por sorteo un obligacionista no sabrá con certeza cuándo su título resultará retirado de la circulación. Es preciso estimar la probabilidad de que el título esté vivo (en circulación) más o menos tiempo.
Definimos el concepto de probabilidad como el resultado de dividir el número de casos favorables de que ocurra un determinado fenómeno concreto (en este caso, amortización de un título) entre el número de casos posibles en una fecha de estudio concreta.
El estudio de probabilidad supone conocer las características del empréstito y en qué momento nos encontramos desde la emisión del mismo. Así, por ejemplo, para un empréstito de N1 emitidos, con una duración de n períodos, realizándose sorteos periódicos en los que se amortizan M1, M2, …, Mn, respectivamente, si quisiéramos hacer un estudio de probabilidad en el momento k desde el origen, gráficamente sería:
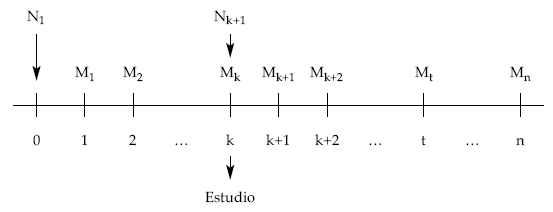
Las probabilidades objeto de estudio más frecuentes son las siguientes:
a) Probabilidad de que un título en circulación a principios de k+1 resulte amortizado en el momento t:
Mt
P = ———
Nk+1
b) Probabilidad de que un título en circulación a principios de k+1 continúe en circulación en el momento t:
Nt+1
P = ———
Nk+1
c) Probabilidad de que un título en circulación a principios de k+1 resulte amortizado en cualquier sorteo hasta el momento t (incluido):
Mk+1 + Mk+2 + … + Mtt Nk+1 – Nt+1 Nt+1
P = ——————————- = —————— = 1 – ——–
Nk+1 Nk+1 Nk+1
A partir del concepto de probabilidad, se puede estimar el tiempo que puede estar en circulación un título adquirido en cualquier momento de tiempo (vida del título), pudiéndose utilizar diferentes promedios entre los que destacamos los siguientes:
- Vida media.
- Vida mediana.
- Vida matemática o financiera.




