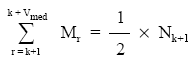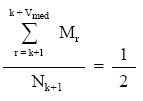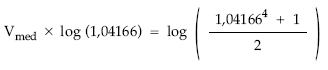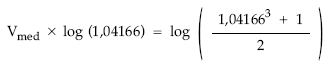Se define como el tiempo que debe transcurrir para que el número de títulos en circulación en la fecha de estudio quede reducido a la mitad o, lo que es lo mismo, el tiempo que ha de transcurrir para que la probabilidad de que un título resulte amortizado en ese intervalo sea 1/2.
Haciendo el estudio en el momento k, tendremos que buscar cuántos sorteos (años) tienen que pasar para que se cumpla la definición de vida mediana, es decir, el número de sorteos que tienen que efectuarse para que se cumplan cualesquiera de las siguientes expresiones:
• El número de títulos amortizados sea la mitad de los que había en circulación en la fecha de estudio:
• La probabilidad de que un título en circulación en la fecha de estudio resulte amortizado en ese intervalo sea 1/2:
Esta forma de calcular resulta aplicable a cualquier empréstito, pero tiene como principal inconveniente la necesidad de conocer el número de títulos en circulación en la fecha de estudio (Nk+1) así como el número de títulos a amortizar desde esa fecha en adelante.
No obstante, para empréstitos con anualidad constante y cupón periódico, constante y vencido (clase I, tipo I) se puede emplear, en el origen, la siguiente expresión simplificada (véase demostración en el anexo II al final del capítulo):
(1 + i)n + 1
(1 + i)Vmed = —————-
2
donde:
i: Tanto del cupón del empréstito.
n: Número de sorteos del empréstito.
Vmed: Vida mediana del empréstito.
método válido si el estudio se realiza en el origen. Para aplicar la fórmula en cualquier momento k, bastará con sustituir n (número de sorteos pendientes) por n–k (número de sorteos pendientes desde la fecha de estudio). Además, si el empréstito tuviera características comerciales, habría que normalizar y la expresión seguirá siendo válida pero cambiando i por i’ (tanto normalizado), resultando:
(1 + i’)n–k + 1
(1 + i’)Vmed = ——————-
2
siendo:
i’: Tanto normalizado del empréstito.
n–k: Número de sorteos pendientes del empréstito.
Vmed: Vida mediana del empréstito.
EJEMPLO 24
Se emite el siguiente empréstito:
- Títulos emitidos: 20.000.
- Nominal título: 1.000 euros.
- Cupón anual: 50 euros.
- Duración: 4 años.
- Prima amortización: 200 euros.
- Anualidad constante.
Se pide:
- Vida mediana en el origen.
- Vida mediana en el momento 1.
Solución:
El cálculo de los títulos amortizados no se realiza ya que se trata del mismo empréstito del ejemplo anterior, por lo que tomamos esa información del mismo.
Vida mediana en el origen
Se trata de determinar cuánto tiempo ha de transcurrir para que el total de títulos emitidos se reduzca a la mitad.
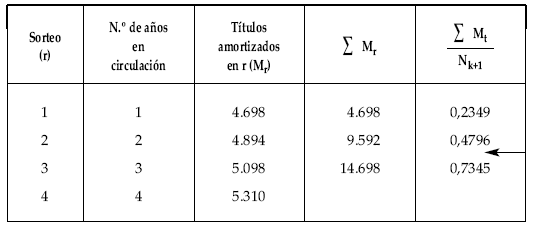
La vida mediana estará comprendida entre 2 y 3, por lo que si se quiere un valor más aproximado habrá que realizar una interpolación lineal:
|
1 ————— 5.098
|
o bien
|
1 ————— (0,4796 – 0,7345)
|
|
t ————— (10.000 – 9.592)
|
t —————- (0,4796 – 0,5)
|
|
|
t = 0,08003
|
t = 0,0800314
|
|
|
Vmed = 2 + t = 2,08003 años
|
Vmed = 2 + t = 2,08003 años
|
Otra posibilidad consistirá en emplear la fórmula antes indicada:
1,041664 + 1
1,04166 Vmed = ——————–
2
Aplicando logaritmos a un miembro y a otro, y teniendo en cuenta las propiedades de los logaritmos, despejaremos la variable buscada:
De donde:
Vmed = 2,08155 años
Vida mediana en el momento 1
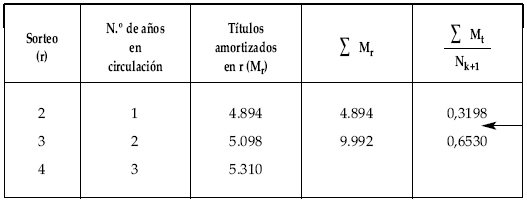
La vida mediana estará comprendida entre los sorteos 2.º y 3.º (1.º y 2.º contados desde la fecha de estudio) por lo que si se quiere un valor más aproximado habrá que realizar una interpolación lineal.
Realizando una interpolación lineal:
|
1 ————— 5.098
|
o bien
|
1 ————— (0,3198 – 0,6530)
|
|
t ————— (7.651 – 4.894)
|
t —————- (0,3198 – 0,5)
|
|
|
t = 0,54080
|
t = 0,54083
|
|
|
Vmed = 1 + t = 1,54080 años
|
Vmed = 1 + t = 1,54080 años
|
Otra posibilidad, mediante la expresión empleada para los empréstitos de estas características:
1,041663 + 1
1,04166 Vmed = ——————–
2
Aplicando logaritmos:
De donde:
Vmed = 1,5459 años