Partiendo de un préstamo cualquiera del que se conocen los componentes del cuadro de amortización (o al menos los pendientes desde la fecha de estudio hasta el final) y que gráficamente responde al siguiente esquema:
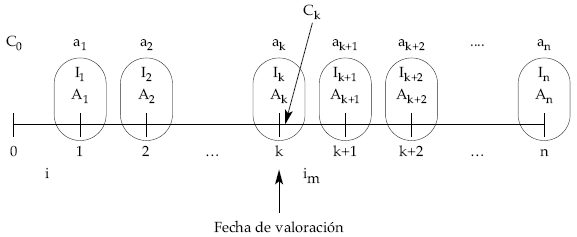
Si nos encontramos en un momento cualquiera k (fecha de valoración), los términos amortizativos pendientes (ak+1, ak+2, …, an) representan para el acreedor (prestamista) un derecho de cobro futuro y para el deudor (prestatario) una obligación de pago. Si en este punto se quisiera cancelar anticipadamente la operación, el deudor debería entregar, en principio, la deuda pendiente (Ck).
Sin embargo, puede ocurrir que las condiciones del mercado hayan cambiado desde que se concertó la operación hasta la fecha actual. En este sentido, para determinar si esta cancelación resulta o no conveniente, sería necesario valorar los términos amortizativos pendientes con un criterio nuevo ajustado a las condiciones actuales, esto es, valorarlos al tanto que en el mercado se está aplicando para operaciones análogas.
Surge la necesidad de valorar el préstamo en condiciones de mercado. La valoración de préstamos implica, pues, conocer las cuantías de los pagos pendientes desde la fecha de estudio y su actualización a dicho momento a un tipo adecuado (tanto de mercado im).
Definiciones:
El acreedor (titular del capital pendiente) puede transferir los derechos que el préstamo por él concedido genera en su conjunto o segregados (por una parte los intereses y por otra el principal): surgen los conceptos de usufructo, nuda propiedad y valor del préstamo.
Usufructo de un préstamo a principios del período k+1, Uk, es el resultado de actualizar al tanto de mercado (im) todas las cuotas de interés pendientes.
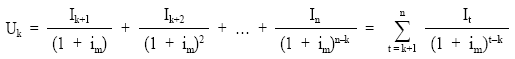
Nuda propiedad de un préstamo a principios del período k+1, Nk, es el resultado de actualizar al tanto de mercado (im) todas las cuotas de amortización pendientes.
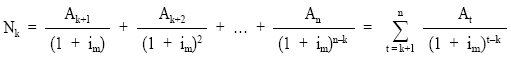
Valor de un préstamo a principios del período k+1, Vk, es el resultado de actualizar al tanto de mercado (im) todos los términos amortizativos pendientes.
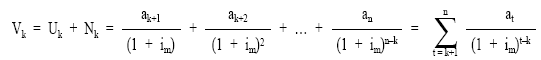
Representa la cantidad que el deudor tendrá que pagar para cancelar su deuda o, desde el punto de vista del prestamista, lo que debería recibir por transferir los derechos futuros que el préstamo supone, en las condiciones actuales del mercado.
Para calcular el importe del valor, usufructo y nuda propiedad de un préstamo bastará con aplicar las definiciones anteriores en la fecha de estudio elegida al préstamo objeto de estudio, debiéndose conocer el tanto de mercado vigente en esa fecha.
EJEMPLO 15
A partir del siguiente préstamo:
- Importe: 100.000 euros.
- Duración: 3 años.
- Tipo de interés: 10% anual.
- Términos amortizativos anuales constantes.
Se pide:
Calcular el valor, usufructo y nuda propiedad transcurrido un año de su concesión si en ese momento el tanto de mercado (im) es del 7%.
Cuadro de amortización:
![]()
|
Años
|
Término amortizativo
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
0
1 2 3 |
40.211,48
40.211,48 40.211,48 |
10.000,00
6.978,85 3.655,59 |
30.211,48
33.232,63 36.555,89 |
30.211,48
63.444,11 100.000,00 |
100.000,00
69.788,52 36.555,89 |
|
Total
|
120.634,44
|
20.634,44
|
100.000,00
|
Cálculo del valor, usufructo y nuda propiedad:
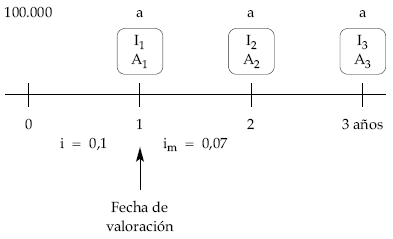
Aplicando las definiciones teóricas:
- Usufructo:
6.978,85 3.655,59
U1 = ————— + ————— = 9.715,22
1,07 1,072 - Nuda propiedad:
33.232,63 36.555,89
N1 = ————— + ————— = 62.987,86
1,07 1,072 - Valor:
40.211,48 40.211,48
V1 = —————- + —————- = 72.703,08
1,07 1,072
También:
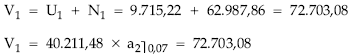
12.1. CASO PARTICULAR: FÓRMULA DE ACHARD
El método de cálculo basado en las definiciones exige conocer las cantidades destinadas al pago de intereses y de amortización en cada momento, desde la fecha de estudio y hasta el final del préstamo.
Un sistema alternativo, más práctico, sería la utilización del sistema de ecuaciones siguiente, que solamente se podrá emplear en el supuesto de que se cumplan los tres siguientes requisitos:
- El tipo de interés del préstamo se mantenga constante desde la fecha de estudio hasta el final.
- El tanto de mercado (im) sea diferente al tanto del préstamo (i).
- El estudio se realice al principio de período.
El sistema es:
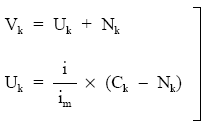
Se trata de un sistema con cuatro incógnitas (V, U, N, C). Para su resolución se calcularán previamente dos de ellas (aplicando las definiciones teóricas) y del sistema se despejarán las dos restantes.
En este sentido, si se trata de un préstamo lineal (cuota de amortización constante), como la cuota de amortización ya se conoce se calcularán previamente (aplicando las definiciones teóricas) el capital vivo (Ck) y la nuda propiedad (Nk) y del sistema se despejará usufructo (Uk) y valor (Nk).
Por el contrario, si se trata de un préstamo francés (término amortizativo constante) o con los términos amortizativos variables en progresión geométrica o aritmética, como los términos amortizativos ya se conocen, se calcularán previamente (aplicando las definiciones teóricas) el capital vivo (Ck) y el valor (Vk) y del sistema se despejará usufructo (Uk) y nuda propiedad (Nk).
| Nota: este sistema de ecuaciones también se puede aplicar cualquiera que sea el sistema de amortización, siempre que se cumplan los tres requisitos anteriores. |
EJEMPLO 16
Resolver el ejemplo anterior aplicando el sistema de ecuaciones.
El sistema se puede aplicar puesto que se cumplen los tres requisitos exigidos, quedando de esta forma:
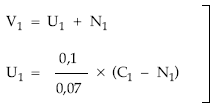
En primer lugar se calcula el capital vivo y valor del préstamo y, del sistema, se despeja usufructo y nuda propiedad:
- Capital vivo:
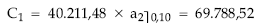
- Valor:
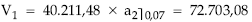
Y a continuación se resuelve el siguiente sistema:
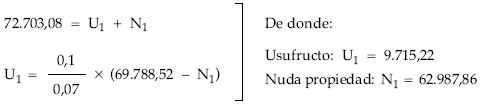
De esta forma, cuando se emplea el sistema no es necesario conocer los elementos del cuadro de amortización, lo que resulta interesante cuando son muchos los períodos aún pendientes hasta la finalización del préstamo.
12.2. VALORACIÓN EN UNA FRACCIÓN DE PERÍODO
Las expresiones anteriores están demostradas para cálculos efectuados en momentos donde tiene lugar amortización de capital (final de período –año–).
Si el cálculo se realizara en cualquier otro momento de tiempo las definiciones siguen siendo válidas pero el sistema práctico de ecuaciones no se podría aplicar directamente.
En este caso, con el sistema práctico se realizarán los cálculos a principios del período y después capitalizaremos hasta la fecha en la que se piden los valores. Esta capitalización se debe efectuar en régimen de compuesta y al tanto de mercado (im).
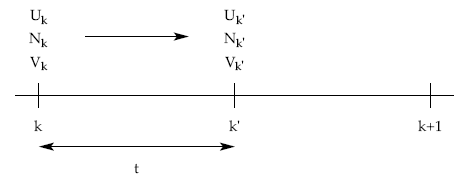
Valor del préstamo en k': Vk' = Vk x (1 + im)t
Nuda propiedad del préstamo en k': Nk' = Nk x (1 + im)t
Usufructo del préstamo en k': Uk' = Uk x (1 + im)t
12.3.
VALORACIÓN DE PRÉSTAMOS CON INTERESES FRACCIONADOS
Cuando nos encontramos con préstamos con intereses fraccionados, habrá que tener en cuenta que el fraccionamiento afecta al usufructo e, indirectamente, al valor, pero no a la nuda propiedad. Para calcular valor, usufructo y nuda propiedad se pueden aplicar, sin más, las definiciones teóricas, pero el sistema de ecuaciones, aunque sigue siendo válido, deberá considerar el efecto del fraccionamiento en el usufructo y en el valor, y quedará de la siguiente forma, si el estudio se hace a principios del período t+1:
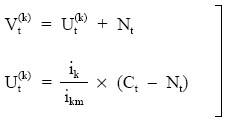
Al tratarse de un préstamo de interés fraccionado, para resolverlo, obligatoriamente, se tendrá que calcular en primer lugar, y fuera del sistema, el capital vivo y la nuda propiedad (a través de las definiciones), y del sistema siempre despejar lo que se ve afectado por el fraccionamiento: usufructo y valor.
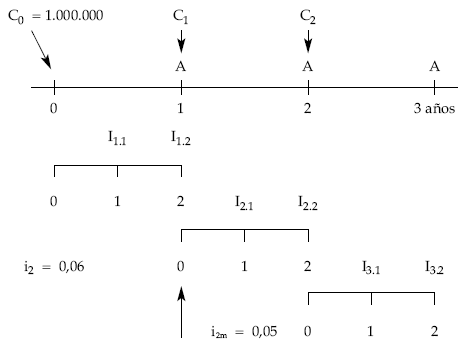
EJEMPLO 17
A partir del siguiente préstamo:
- Importe: 300.000 euros.
- Duración: 3 años.
- Cuotas de amortización anuales constantes.
- Intereses semestrales al 6% efectivo semestral.
Se pide:
Calcular valor, usufructo y nuda propiedad transcurrido un año de su concesión si en ese momento el tanto de mercado ( im) es del 5% efectivo semestral.
Cuadro de amortización:
300.000,00
A = —————– = 100.000,00
3
|
Períodos
|
Capital vivo
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Términos
amortizativos |
|
1.1.
1.2. |
300.000,00
300.000,00 |
18.000,00
18.000,00 |
–
100.000,00 |
–
100.000,00 |
18.000,00
118.000,00 |
|
2.1.
2.2. |
200.000,00
200.000,00 |
12.000,00
12.000,00 |
–
100.000,00 |
100.000,00
200.000,00 |
12.000,00
112.000,00 |
|
3.1.
3.2. |
100.000,00
100.000,00 |
6.000,00
6.000,00 |
–
100.000,00 |
200.000,00
300.000,00 |
6.000,00
106.000,00 |
|
Total
|
|
72.000,00
|
300.000,00
|
|
372.000,00
|
Cálculo del valor, usufructo y nuda propiedad:
1.er caso: aplicando las definiciones teóricas.
- Usufructo:
12.000 12.000 6.000 6.000
U21 = ———– + ———– + ———- + ———- = 32.432,17
1,05 1,052 1,053 1,054 - Nuda propiedad:
100.000 100.000
N1 = ————– + ————- = 172.973,20
1,052 1,054 - Valor:
V 21 = U21 + N1 = 32.432,17 + 172.973,20 = 205.405,37
2.º caso: aplicando el sistema de ecuaciones.
El sistema se puede aplicar puesto que se cumplen los dos requisitos exigidos, quedando de esta forma:
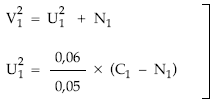
En primer lugar se calcula el capital vivo y nuda propiedad y, del sistema, se obtiene el usufructo y el valor:
- Capital vivo:
C1 = 2 x A = 200.000
- Nuda propiedad:
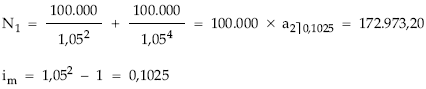
Y a continuación se resuelve el siguiente sistema:
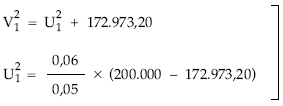
Por tanto:
0,06
U21 = ——— x [200.000 – 172.973,20] = 32.432,17
0,05
V21 = 32.432,17 + 172.973,20 = 205.405,37




