La definición de tantos equivalentes es la misma que la vista en régimen de simple, esto es, dos tantos cualesquiera, expresados en distintas unidades de tiempo, son tantos equivalentes cuando aplicados a un mismo capital inicial y durante un mismo período de tiempo producen el mismo interés o generan el mismo capital final o montante.
Como ya se comentó cuando se hablaba del interés simple, la variación en la frecuencia del cálculo (y abono) de los intereses suponía cambiar el tipo de interés a aplicar para que la operación no se viera afectada finalmente. Entonces se comprobó que los tantos de interés equivalentes en simple son proporcionales, es decir, cumplen la siguiente expresión:
i = ik x k
Sin embargo, esta relación de proporcionalidad no va a ser válida en régimen de compuesta, ya que al irse acumulando los intereses generados al capital de partida, el cálculo de intereses se hace sobre una base cada vez más grande; por tanto, cuanto mayor sea la frecuencia de capitalización antes se acumularán los intereses y antes generarán nuevos intereses, por lo que existirán diferencias en función de la frecuencia de acumulación de los mismos al capital para un tanto de interés dado.
Este carácter acumulativo de los intereses se ha de compensar con una aplicación de un tipo más pequeño que el proporcional en función de la frecuencia de cómputo de intereses. Todo esto se puede apreciar en el siguiente ejemplo, consistente en determinar el montante resultante de invertir 1.000 euros durante 1 año en las siguientes condiciones:
- Interés anual del 12%
Cn = 1.000 x (1 + 0,12)1 = 1.120,00
- Interés semestral del 6%
Cn = 1.000 x (1 + 0,06)2 = 1.123,60
- Interés trimestral del 3%
Cn = 1.000 x (1 + 0,03)4 = 1.125,51
Los resultados no son los mismos, debido a que la capitalización de los intereses se está realizando con diferentes frecuencias manteniendo la proporcionalidad en los diferentes tipos aplicados.
Para conseguir que, cualquiera que sea la frecuencia de capitalización, el montante final siga siendo el mismo es necesario cambiar la ley de equivalencia de los tantos.
2.1. RELACIÓN DE TANTOS EQUIVALENTES EN COMPUESTA
Los tantos en compuesta para que resulten equivalentes han de guardar la siguiente relación:
1 + i = (1 + ik)k
donde k es la frecuencia de capitalización, que indica:
- El número de partes iguales en las que se divide el período de referencia que se tome (habitualmente el año).
- Cada cuánto tiempo se hacen productivos los intereses, esto es, cada cuánto tiempo se acumulan los intereses, dentro del período, al capital para producir nuevos intereses.
Esta relación se obtiene a partir de la definición de equivalencia vista anteriormente, obligando a que un capital (C0) colocado un determinado período de tiempo (n años) genere el mismo montante (Cn) con independencia de la frecuencia de acumulación de intereses (i o ik):
Utilizando el tanto anual i, el montante obtenido será:
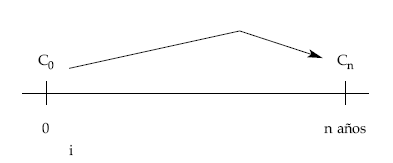
Cn = C0 x (1 + i)n
Utilizando el tanto k-esimal ik, el montante obtenido será:
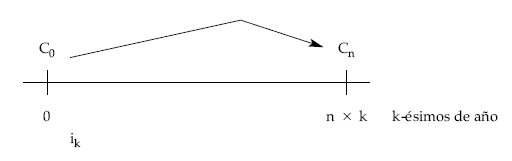
Cn = C0 x (1 + ik)nk
Si queremos que el montante sea el mismo en los dos casos, se tiene que producir la igualdad entre los resultados de ambas operaciones, esto es, dado que la operación es la misma –ya que lo único que ha cambiado es la frecuencia de cálculo de los intereses–, se debe conseguir el mismo capital final en ambos casos, por tanto, obligando a que se cumpla esa igualdad de montantes:
C0 x (1 + i)n = C0 x (1 + ik)nk
Simplificando la igualdad, eliminando C0 y la potencia n:
C0 x (1 + i)n = C0 x (1 + ik)nk
Quedando finalmente:
| (1 + i ) = (1 + ik)k |
Expresión que indica la relación en la que han de estar los tantos, i e ik, para que produzcan el mismo efecto, es decir, para que sean equivalentes.
El valor de i en función de ik será:
| i = (1 + ik)k – 1 |
El valor de ik en función de i será:
| ik = (1 + i)1/k – 1 |
EJEMPLO 6
Determinar el montante resultante de invertir 1.000 euros durante 1 año a un tanto del 12% efectivo anual, suponiendo:
- Devengo anual de intereses:
i = 0,12
Cn = 1.000 x (1 + 0,12)1 = 1.120,00 € - Devengo semestral de intereses:
Puesto que el tipo que se conoce es anual y ahora la frecuencia de cálculo es semestral, habrá que calcular previamente el tanto semestral equivalente al anual de partida, para después calcular el montante.
i2 = (1 + 0,12)1/2 – 1 = 0,05830
Cn = 1.000 x (1 + 0,05830)2 = 1.120,00 € - Devengo trimestral de intereses:
Igual que en el caso anterior, habrá que calcular el tanto trimestral equivalente al anual conocido.
i4 = (1 + 0,12)1/4 – 1 = 0,028737
Cn = 1.000 x (1 + 0,028737)4 = 1.120,00 €
Los resultados son los mismos, debido a la utilización de intereses equivalentes.




