El empréstito, como operación financiera, supone la existencia de una equivalencia financiera entre una prestación (el nominal del empréstito) y una contraprestación (el conjunto de capitales que se desembolsan para su total devolución). Dicha equivalencia se cumple para un tipo de interés que, de no existir ningún componente además del cupón, coincide con el tipo al que se calcula el cupón (si es constante) acordado en la emisión.
El problema surge cuando existen «características comerciales» en el empréstito, es decir, otras partidas que afectan a la prestación y/o a la contraprestación haciendo que se modifique el valor financiero de las mismas, no cumpliéndose la equivalencia para el tipo de interés contractual. Es decir, cuando en la operación, además de devolverse el capital y pagarse cupones, existen otros pagos y cobros de diferente naturaleza que hacen que la equivalencia entre pagos y cobros no se cumpla al tipo del cupón.
Surge así la necesidad de calcular un nuevo tipo que permita enfrentar las cantidades «realmente» entregadas y recibidas en la operación, tanto para el acreedor (obligacionistas) como para el deudor (emisor). Este nuevo tipo será una medida real (efectiva) de la rentabilidad obtenida por el prestamista –obligacionista– y del coste total (efectivo) soportado por el deudor –emisor–, por todo aquello que afecte a una y otra parte, respectivamente.
8.1. TANTO EFECTIVO DEUDOR O DEL EMISOR (ie)
Será una medida del coste real (coste financiero) que supone para el emisor la emisión y posterior devolución del empréstito, considerando además de los intereses de los cupones todos los gastos soportados en la operación, cualquiera que sea su naturaleza (lotes, primas –de emisión o reembolso– y gastos –de emisión o administración–).
Se obtendrá a partir de la siguiente equivalencia financiera para el emisor:
|
LO REALMENTE RECIBIDO
(Valor de emisión del empréstito) |
<——>
ie |
LO REALMENTE PAGADO
(Gastos de emisión y anualidades teóricas) |
8.2.
TANTO EFECTIVO ACREEDOR O DEL CONJUNTO DE OBLIGACIONISTAS (io)
Proporciona una medida de la rentabilidad media obtenida por el conjunto de obligacionistas, considerando todas aquellas partidas que influyen en la misma.
Se obtendrá a partir de la equivalencia financiera que considera todo lo que paga el conjunto de obligacionistas y todo lo que recibe este colectivo a lo largo de todo el empréstito:
|
LO REALMENTE PAGADO
(Valor de emisión del empréstito) |
<——>
io |
LO REALMENTE RECIBIDO
(Anualidades teóricas sin gastos de administración) |
8.3. RENTABILIDAD DE UN TÍTULO TIR (r)
También proporciona una medida de rentabilidad, en este caso para un título en cuestión y no para el conjunto de títulos emitidos (tanto obligacionista).
Para ello sólo se tendrán en cuenta los flujos originados desde la compra (en la suscripción) hasta su amortización en un momento determinado para el título elegido.
|
LO REALMENTE PAGADO
(Valor de emisión del título) |
<——>
r |
LO REALMENTE RECIBIDO
[Cupones,valor de reembolso y lote (si hay)] |
EJEMPLO 21
Se emite el siguiente empréstito:
- Títulos emitidos: 75.000.
- Nominal título: 1.000 euros.
- Cupón anual: 120 euros.
- Duración: 10 años.
- Sorteos anuales, amortizándose los títulos con prima de 200 euros.
- Los títulos se adquieren al 90%.
- Gastos iniciales de 500.000 euros a cargo del emisor.
- Gastos de administración del 1‰ sobre las cantidades pagadas anualmente a los obligacionistas.
- Anualidad constante.
Se pide:
- Anualidad del empréstito.
- Tanto efectivo emisor.
- Tanto efectivo obligacionista.
- TIR de un título que se amortiza en el 5.º sorteo.
Solución:
Cálculo de la anualidad
Empréstito de cupón periódico constante y anualidad constante que además incluye una prima de amortización y unos gastos de administración. La estructura es la siguiente:
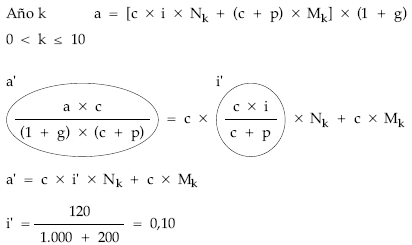
Planteando la equivalencia en origen:
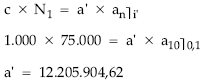
deshaciendo el cambio de variable:
a x c
a’ = ———————
(1 + g) x (c + p)
obtenemos la anualidad real:
a x 1.000
12.205.904,62 = ——————–
1,001 x 1.200
a = 14.661.732,62
Tanto efectivo emisor
|
LO RECIBIDO
|
ie?
<—–> |
LO PAGADO
|
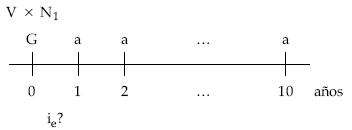
Planteando la equivalencia en el origen entre lo cobrado (V x N1) y todo lo pagado en la operación (G y a) por el emisor, resulta el tanto efectivo emisor ie.
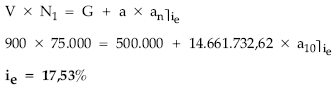
Para despejar el tanto se puede emplear una máquina financiera, tantear hasta lograr una solución que se aproxime o bien emplear tablas financieras de ![]()
Tanto efectivo obligacionista
La anualidad que paga el emisor incorpora unos gastos de administración que no son cobrados por los obligacionistas, por lo que habrá que eliminar del término amortizativo esos gastos quedando la expresión:
a
——–
1 + g
|
LO PAGADO
|
io?
<—–> |
LO RECIBIDO
|
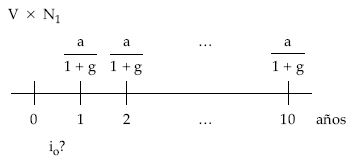
Planteando la equivalencia en el origen entre lo pagado (V x N1) y todo lo cobrado en la operación (a/1 + g) por los obligacionistas, resulta el tanto efectivo obligacionista io.
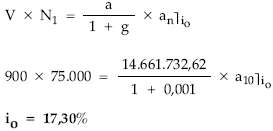
TIR de un título amortizado en el 5.º sorteo
|
LO PAGADO
|
r
<—–> |
LO RECIBIDO
|
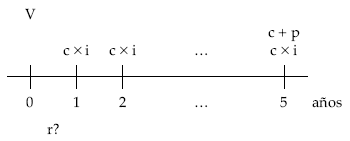
Planteando la equivalencia en el origen entre lo pagado por el título (V) y todo lo cobrado hasta su amortización (c x i y c + p), resulta el tanto TIR (r).
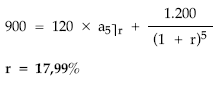
Para el cálculo del TIR no se podrán usar tablas financieras, quedando como únicas alternativas bien la máquina financiera o el tanteo.
EJEMPLO 22
Se emite el siguiente empréstito:
- Títulos emitidos: 50.000.
- Nominal del título: 1.000 euros.
- No abono de cupones anuales, acumulándose hasta el momento del sorteo al 13%.
- Sorteos anuales, repartiéndose un premio de 1.000 euros para cada una de las 100 primeras obligaciones sorteadas cada año.
- Gastos de emisión: 1.000.000 de euros.
- Gastos de administración del 1‰ sobre las cantidades pagadas anualmente a los obligacionistas.
- Duración: 15 años.
- Emisión de los títulos al 95% de su valor nominal.
- Anualidad constante.
Se pide:
- Anualidad del empréstito.
- Tanto efectivo emisor.
- Tanto efectivo obligacionista.
- Rentabilidad de un título adquirido en la emisión y amortizado en el 6.º sorteo con lote.
Solución:
Cálculo de la anualidad
Empréstito de cupón constante acumulado en compuesta, anualidad constante, con lote y gastos de administración. La estructura de la anualidad será:
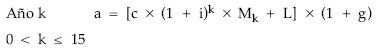
Normalizando:
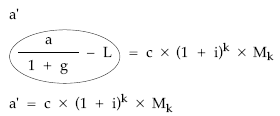
Planteando la equivalencia en 0:
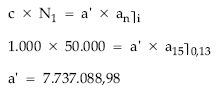
deshaciendo el cambio de variable:
a
a’ = ——— – L
1 + g
se obtiene la anualidad real:
a
7.737.088,98 = ——— – 100.000 a = 7.844.926,07
1,001
Tanto efectivo emisor
|
LO RECIBIDO
|
ie?
<—–> |
LO PAGADO
|
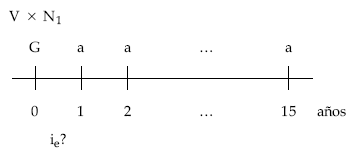
Planteando la equivalencia en el origen entre lo cobrado (V x N1) y todo lo pagado en la operación (G y a) por el emisor, resulta el tanto efectivo emisor ie.
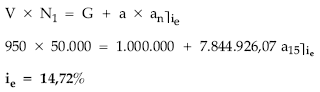
Tanto efectivo obligacionista
|
LO PAGADO
|
io?
<—–> |
LO RECIBIDO
|
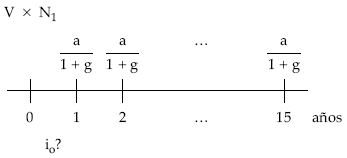
Planteando la equivalencia en el origen entre lo pagado (V x N1) y todo lo cobrado en la operación (a/i + g) por los obligacionistas, resulta el tanto efectivo obligacionista io.
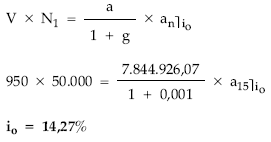
TIR de un título amortizado en el 6.º sorteo con lote
|
LO PAGADO
|
r
<—–> |
LO RECIBIDO
|
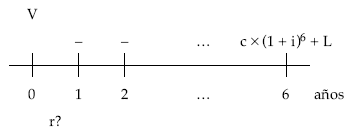
?Planteando la equivalencia en el origen entre lo pagado por el título (V) y todo lo cobrado en la amortización [c x (1 + i)6 + L], resulta el tanto TIR (r).
1.000 x 1,136 + 1.000
950 = —————————–
(1 + r)6
r = 21,67%




