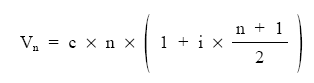Se trata de valorar un conjunto de capitales con vencimientos equidistantes en un determinado momento pero la duración de la operación no supera el año, por tanto, se trata de operaciones a realizar en régimen de simple.
A diferencia de lo que ocurría con las rentas valoradas en régimen de compuesta, en las rentas en simple (que emplean leyes financieras en régimen de simple), por las particularidades de este tipo de leyes, habrá que distinguir a la hora de calcular valores actuales y finales. De hecho, solamente se obtienen expresiones fáciles de emplear cuando los valores actuales se realizan a tipo de descuento y los valores finales a tipo de interés.
7.1. VALOR ACTUAL
Para el caso de una renta pospagable, temporal, constante, inmediata y entera valorada a un tipo de descuento (d) la situación será:
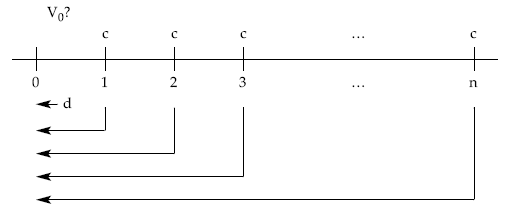
Aplicando la definición de valor actual empleando descuentos comerciales simples:
V0 = c x (1 – d) + c x (1 – 2d) + c x (1 – 3d) + … + c x (1 – nd)
Simplificando:
V0 = c x [(1 + 1 + … + 1) – (d + 2d + 3d + … + nd)]
Dentro del corchete el primer paréntesis es una suma de n veces la unidad y el segundo es una suma de n términos en progresión aritmética, por tanto:
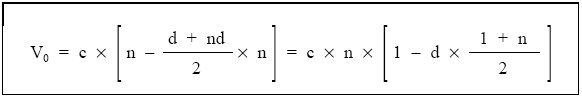
Si, en cambio, la renta fuera prepagable, manteniéndose las demás características sin cambios, el cálculo será:
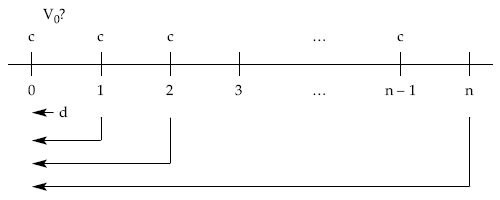
Aplicando la definición de valor actual empleando descuentos comerciales simples:
V0 = c + c x (1 – d) + c x (1 – 2d) + c x (1 – 3d) + … + c x [1 – (n – 1) d]
Simplificando, igual que en el caso anterior:
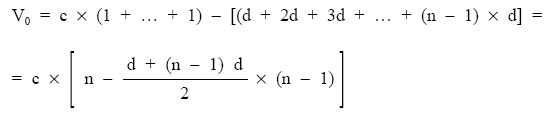
Finalmente:
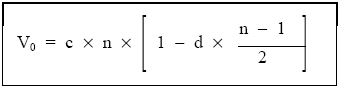
A idénticos resultados hubiéramos llegado si en lugar de calcular los valores actuales de los n capitales iguales hubiéramos considerado un único capital igual a la suma de todos ellos, que se hiciese efectivo en el vencimiento medio.
En efecto, para el caso de términos, n términos pospagables, el vencimiento medio vendría dado por:
1 + 2 + 3 + … + n
Vm = ————————–
n
Siendo el numerador la suma de n términos en progresión aritmética que será la semisuma de los extremos por el número de términos, queda:
(1 + n) x n
—————
2 (1 + n) x n n + 1
Vm = —————— = —————— = ———
n 2n 2
Por tanto, habrá que descontar desde ese punto un único capital de cuantía c x n:
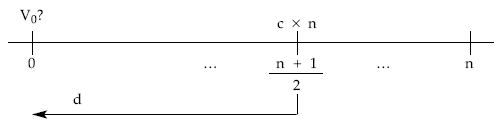
resultando:
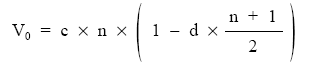
En el caso de capitales prepagables, el vencimiento medio sería:
[0 + (n – 1)] x n
———————-
0 + 1 + 2 + 3 + … + (n – 1) 2
Vm = ————————————- = ———————-
n n
(n – 1) x n n – 1
Vm = —————————– = ——————-
2n 2
Por tanto, habrá que descontar desde ese punto un capital único de cuantía c x n:
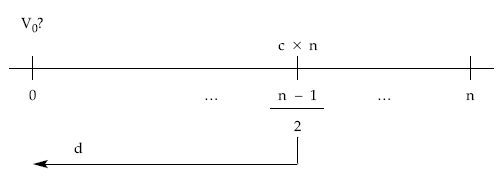
Obteniendo el mismo resultado que moviendo los capitales uno a uno:
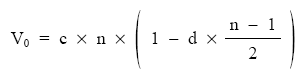
EJEMPLO 20
Calcular el valor actual de la siguiente renta:
- Duración: 1 año.
- Términos cuatrimestrales de 100 euros.
- Tipo de descuento: 2% simple cuatrimestral.
a) Suponiendo términos vencidos.
b) Suponiendo términos prepagables.
a) Términos vencidos:
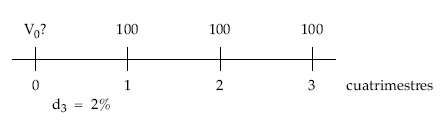
Desplazando los capitales uno a uno:
V0 = 100 x (1 – 0,02) + 100 x (1 – 2 x 0,02) + 100 x (1 – 3 x 0,02) = 288 €
Aplicando la fórmula:
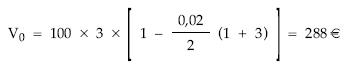
b) Términos prepagables:
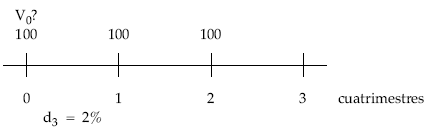
Desplazando los capitales uno a uno:
V0 = 100 + 100 x (1 – 0,02) + 100 x (1 – 2 x 0,02) = 294 €
Aplicando la fórmula:
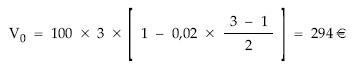
7.2. VALOR FINAL
Para el caso de una renta pospagable, temporal, constante, inmediata y entera la situación será:
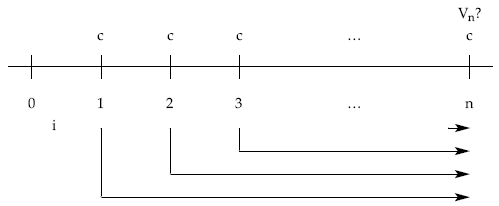
Aplicando la definición de valor final empleando capitalización simple:
Vn = c + c x (1 + i) + c x (1 + 2i) + c x (1 + 3i) + … + c x [1 + (n – 1) i]
Simplificando:
Vn = c x [(1 + … + 1) + (i + 2i + 3i + … + (n – 1)) i]
Dentro del corchete el primer paréntesis es una suma de n veces la unidad y el segundo es una suma de n–1 términos en progresión aritmética (semisuma de los extremos multiplicando por el número de términos), por tanto:
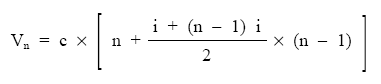
Resultando finalmente:
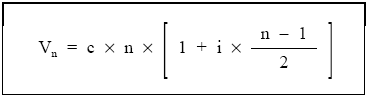
En el caso de una renta prepagable, manteniéndose sin cambios las demás características:
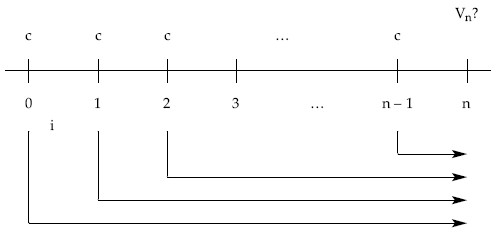
Aplicando la definición de valor final empleando capitalización simple:
Vn = c x (1 + i) + c x (1 + 2i) + c x (1 + 3i) + … + c x (1 + ni)
Simplificando:
Vn = c x [(1 + … + 1) + (i + 2i + 3i + … + ni)]
Siendo el primer paréntesis n y el segundo la suma de n términos en progresión aritmética i + ni/2 x n, resulta:
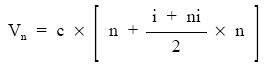
Finalmente:
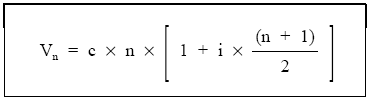
A idénticos resultados hubiéramos llegado si en lugar de calcular los valores finales de los n capitales iguales hubiéramos considerado un único capital igual a la suma de todos ellos, que se hiciese efectivo en el vencimiento medio.
En efecto, para el caso de n términos pospagables, el vencimiento medio vendría dado por:
1 + 2 + 3 + … + n
Vm = ————————–
n
Operando en el numerador:
(1 + n) x n
—————-
2 (1 + n) x n n + 1
Vm = ——————– = —————— = —————-
n 2n 2
Por tanto, habrá que capitalizar desde ese punto un capital único de cuantía c x n:
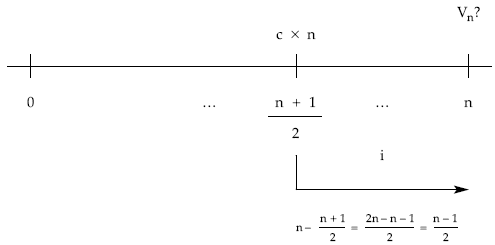
Resultando:
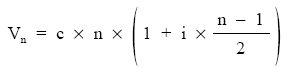
En el caso de capitales prepagables, el vencimiento medio sería:
[0 + (n – 1)] x n
———————-
0 + 1 + 2 + 3 + … + (n – 1) 2 (n – 1) x n
Vm = ————————————- = ————————– = ——————–
n n s2n
n – 1
Vm = ————–
2
Por tanto, habrá que capitalizar desde ese punto un capital único de cuantía c x n:
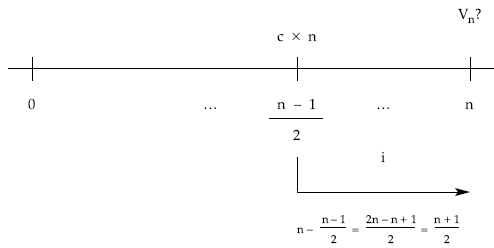
obteniendo el mismo resultado que moviendo los capitales uno a uno: