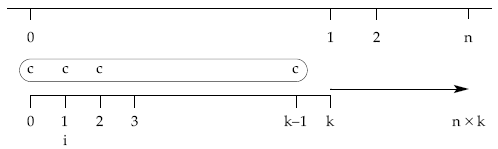
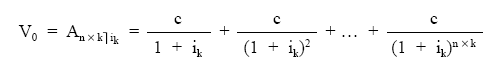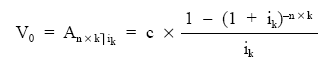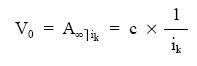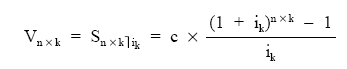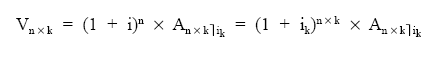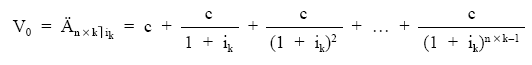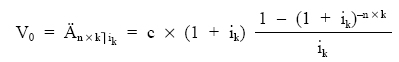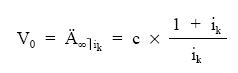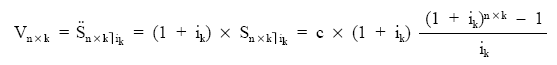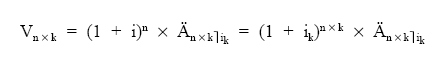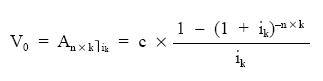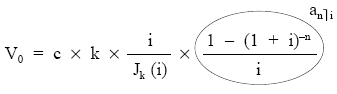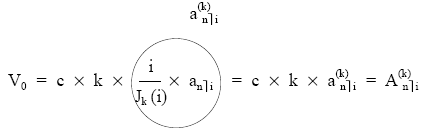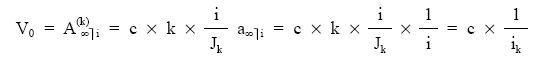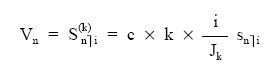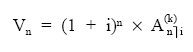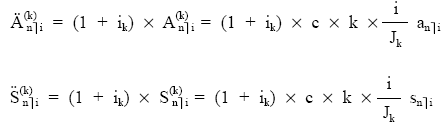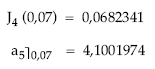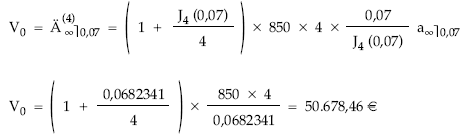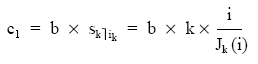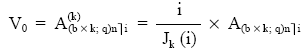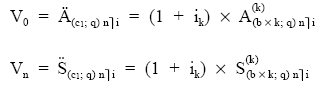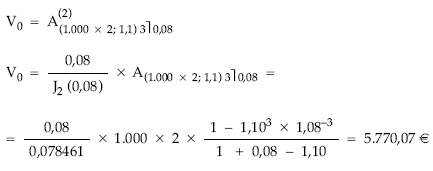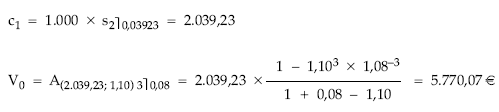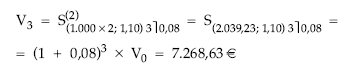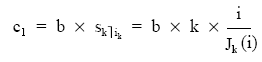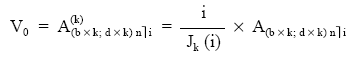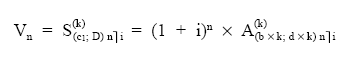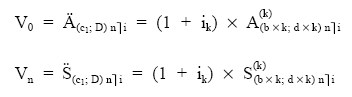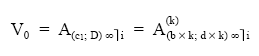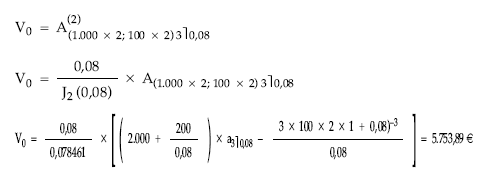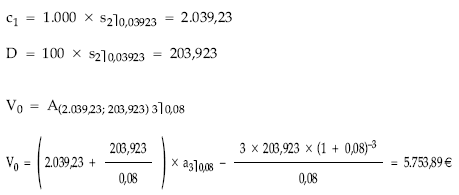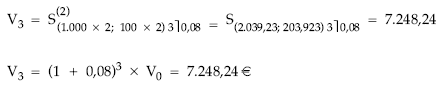El fraccionamiento de las rentas consiste en dividir cada período de varios sub-períodos (k) asociando a cada subperíodo un capital. Por tanto, el fraccionamiento de una renta de n períodos la transforma en otra de n x k términos referidos a otros tantos subperíodos.
A la hora de estudiar este tipo de rentas distinguiremos entre:
- Rentas fraccionadas constantes.
- Rentas fraccionadas en progresión geométrica.
- Rentas fraccionadas en progresión aritmética.
Todas las fórmulas vistas hasta ahora son válidas para rentas enteras, ya fueran constantes o variables. Pero, ¿servirán para cuando la renta es fraccionada? La respuesta es afirmativa, siempre que se hagan los ajustes previos para convertirlas en rentas enteras.
5.1. RENTAS FRACCIONADAS CONSTANTES
Son aquellas en las que la unidad de tiempo en la que viene expresado el tanto de interés de la renta es mayor que el tiempo del término, cualquiera que sea una y otra.
Para resolver este tipo de rentas fraccionadas se puede proceder de dos formas distintas, que lógicamente llegan al mismo resultado final:
- Utilizando el tanto equivalente.
- Utilizando el factor de transformación (o de conversión).
5.1.1. Método del tanto equivalente
Se trata de transformar el tipo de interés del problema en otro equivalente en la misma unidad de tiempo que los capitales de la renta.
5.1.1.1. Rentas fraccionadas pospagables
Haciendo el estudio para el caso de una renta temporal de n períodos, siendo los términos constantes de frecuencia k, vencidos e inmediata y el tanto de valoración i (en la unidad del período), la representación gráfica será:

En primer lugar, a partir del tipo de interés i se calcula el tanto equivalente que venga expresado en la unidad de los capitales (k-ésimos), para ello utilizaremos la relación de tantos equivalentes en compuesta:
ik = (1 + i)1/k – 1
Resultando una renta constante (de cuantía c), temporal (de n x k términos), pospagable, inmediata y entera (al tanto ik):

Si queremos calcular el valor actual se deberían actualizar a un tanto ik todos los capitales:
Finalmente:
Para el caso de renta perpetua:
El valor final se calculará, bien valorando los términos uno a uno hasta el final de la renta al tanto ik, quedará de la siguiente forma:
o bien capitalizando el valor actual previamente calculado:
EJEMPLO 13
Determinar el valor actual de una renta de 5 años de duración, siendo el tanto de valoración el 7% efectivo anual y sus términos de 850 euros trimestrales pospagables.
Al venir el tipo de la renta en años y los términos en trimestres, la renta es fraccionada. Teniendo otras características: constante, temporal (20 términos trimestrales), pospagable e inmediata.
Para su cálculo se convierte el tipo anual en un tipo trimestral equivalente, tratándose como una renta entera.

5.1.1.2. Rentas fraccionadas prepagables
Si seguimos la renta del caso anterior, pero introduciendo un único cambio consistente en que los capitales se sitúan al principio de cada subperíodo, la situación queda así:
resultando una renta constante (de cuantía c), temporal (de n x k términos), prepagable, inmediata y entera (al tanto ik):
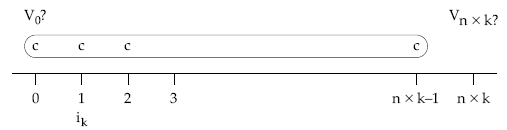
El valor actual se calcula actualizando a un tanto ik todos los capitales:
Finalmente:
Para el caso de renta perpetua:
El valor final se calculará, a partir de los términos de la renta, uno a uno hasta el final de la renta al tanto ik:
o bien capitalizando el valor actual previamente calculado:
5.1.2. Método del factor de transformación
En este caso se trata de emplear los datos del problema y la información complementaria que se suministraría. En principio, lo normal será contar con tablas de valores actuales unitarios (anùi) , y de tantos nominales [Jk (i)], referidos al tanto i del supuesto.
Haciendo el estudio para el caso de una renta temporal de n períodos, siendo los términos constantes de frecuencia k, vencidos e inmediata y el tanto de valoración i (en la unidad del período). La representación gráfica será:
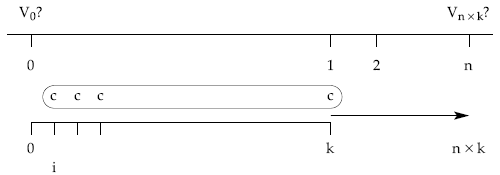
Para el cálculo del valor actual partimos de la expresión empleada anteriormente con el método del tanto equivalente:
Pero ahora, en lugar de utilizar el tanto ik y trabajar con una renta de n x k términos, vamos a tener en cuenta las siguientes expresiones:
• La relación de tantos equivalentes en compuesta:
(1 + i) = (1 + ik)k
que generalizando para n períodos y elevando ambos miembros a (–1), queda:
(1 + i)-n = (1 + ik)-n x k
• El tanto nominal equivalente al tipo efectivo i:
Jk (i)
que nos permite conocer ik a partir del nominal:
Jk (i)
ik = ———–
k
sustituyendo estos cambios en el valor actual de partida queda:
1 – (1 + i)-n 1 – (1 + i)-n
V0 = c x ——————- = c x k x ——————–
Jk (i) Jk (i)
———
k
Si multiplicamos y dividimos el segundo miembro por i:
simplificando, queda:
siendo el cociente:
i
———–
Jk (i)
el denominado factor de transformación.
Al mismo resultado se hubiera llegado si sustituimos los k términos de un período por un único capital equivalente expresado en la unidad del tanto i y repitiendo esa operación para el resto de períodos se habrá convertido la renta en entera (tanto de valoración y términos de la renta en la misma unidad de tiempo –en la unidad del tipo de interés de partida–). Este capital equivalente puede tomarse al final del período (pospagable) o al principio (prepagable), sin que eso afecte al resultado final.
Así, si el capital equivalente se considera pospagable, será el valor final de la renta formada por los k términos fraccionados constantes llevados al final de período:
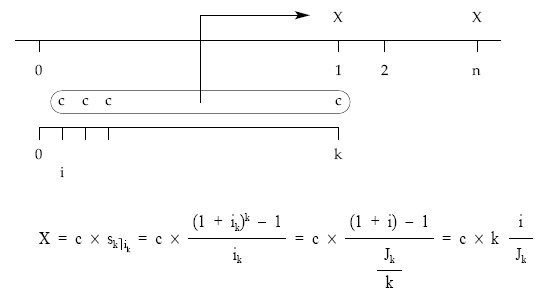
Una vez calculado X, se trataría de actualizar una renta constante, de n términos de cuantía X, pospagable y entera.
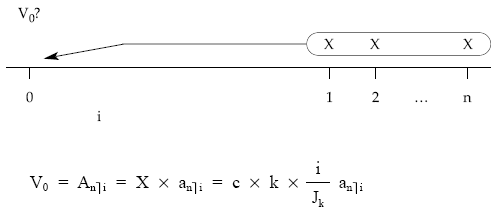
Para el caso de renta perpetua:
El valor final se calculará, bien valorando los términos uno a uno hasta el final de la renta al tanto ik:
o bien capitalizando el valor actual previamente calculado:
Para rentas prepagables:
EJEMPLO 14
Se trata de resolver el ejemplo anterior a través del factor de transformación, por tanto, se pide el valor actual de una renta de 5 años de duración, siendo el tanto de valoración el 7% efectivo anual y sus términos de 850 euros trimestrales pospagables.
Contamos con la siguiente información adicional:
EJEMPLO 15
Determinar el valor actual de una renta perpetua, siendo el tanto de valoración el 7% efectivo anual y sus términos de 850 euros trimestrales prepagables. Se dispone, como información adicional, del tanto nominal trimestral equivalente al 7% efectivo anual: J4 (0,07) = 0,0682341.
Es una renta constante, perpetua, prepagable, inmediata y fraccionada (tanto de valoración anual y términos trimestrales).
5.2.
RENTAS FRACCIONADAS VARIABLES EN PROGRESIÓN GEOMÉTRICA
Son aquellas en las que los términos siguen una progresión pero la razón de la variación se produce en una unidad de tiempo mayor que aquella en la que vienen dados los capitales, cualquiera que sea el tipo de interés de la renta. Por ejemplo, el caso de la renta formada por las nóminas de un individuo que cobra mensualmente y tiene subidas salariales anuales calculadas sobre el sueldo del año anterior: los sueldos varían anualmente pero se mantienen constantes dentro del año.
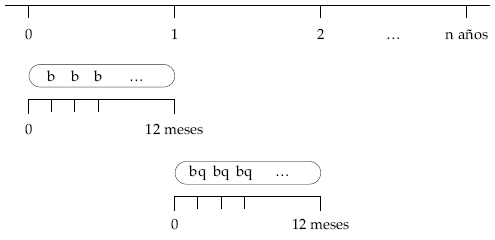
Conviene recordar que las fórmulas de las rentas en geométrica utilizadas sólo se pueden aplicar cuando los términos, el tanto de valoración y la razón de la renta están expresados en la misma unidad (obligatoriamente la de la razón, para que haya progresión).
Por tanto, el ejemplo anterior (y cualquier caso parecido) no se podría resolver aplicando directamente las fórmulas de las rentas en progresión geométrica sin más.
Deberemos trabajar obligatoriamente en la unidad de tiempo en la que se produce la variación de los capitales (la unidad de la razón), lo que supondrá transformar, si es necesario, el tanto de valoración del problema (a través de la expresión de tantos equivalentes en compuesta). Por lo que se refiere a los capitales, éstos se mantienen constantes a nivel de subperíodo, dentro de cada período, y sólo varían de un período a otro (en el caso del ejemplo anterior, los sueldos se mantienen constantes dentro del año y varían de un año para otro), y de la misma manera que se cambia el tipo de interés, se deberán sustituir los términos por otros equivalentes en la unidad de la razón de la progresión.
En el ejemplo de partida, la situación quedará gráficamente como sigue:
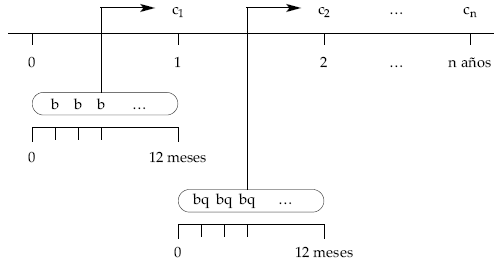
Se calculan términos anuales equivalentes a los términos constantes k-esimales:
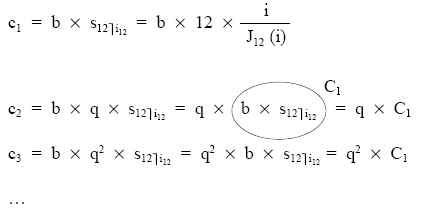
No obstante, bastará con obtener el primero de ellos, porque según se observa los demás varían en progresión con la razón de partida (q).
Con carácter más general, una renta variable en progresión geométrica de razón q, con términos k fraccionados, pospagables, temporal (de n períodos), al tanto i de valoración, la representación será la siguiente:
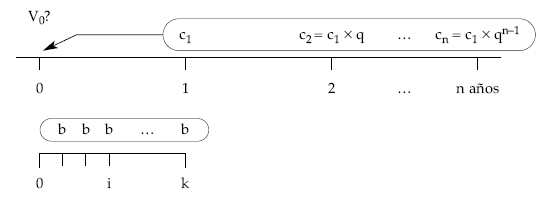
El cálculo del primer término equivalente c1 será:
y a continuación se tratará como una renta en progresión geométrica entera.
5.2.1. Valor actual
Si se quiere emplear una terminología en la que se aprecie el fraccionamiento, la expresión del valor actual queda así:
Siendo:
k: la frecuencia de fraccionamiento.
b x k:
la suma aritmética de los capitales del primer período de la renta.
q: la razón de la progresión.
n: el número de períodos (en la unidad de tiempo de la razón).
i: el tipo de interés en la unidad de tiempo de la razón.
A partir del valor actual pospagable se puede obtener el resto de valores: prepagable, final, perpetuo, diferido y anticipado, sin más que tener las consideraciones ya comentadas para estos cálculos en cualquier tipo de renta.
5.2.2. Valor final
5.2.3. Prepagable
Es importante resaltar el hecho de que en las rentas prepagables, cuando se convierten en pospagables multiplicando por (1 + tipo de interés) habrá que hacerlo con el tanto en el que vienen los capitales (1 + ik).
5.2.4. Perpetua
EJEMPLO 16
Calcular el valor actual de la siguiente renta:
- Duración: 3 años.
- Términos semestrales vencidos de 1.000 euros durante el primer año.
- Aumento anual acumulativo de los términos de un 10%.
- Tanto de valoración del 8% efectivo anual.
Se trata de una renta variable en progresión geométrica (aumento de tipo acumulativo) por años, con términos semestrales vencidos (fraccionada), temporal e inmediata.
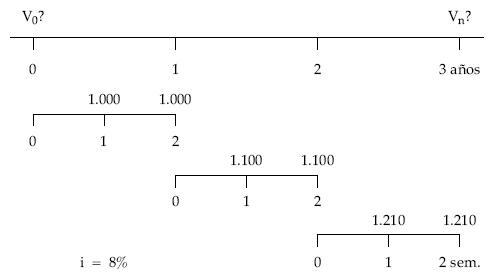
• Cálculo del valor actual empleando la terminología del fraccionamiento:
• Cálculo del valor actual empleando el término equivalente:
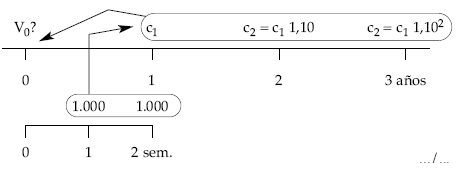
• Cálculo del valor final:
5.3.
RENTAS FRACCIONADAS VARIABLES EN PROGRESIÓN ARITMÉTICA
Al igual que en el caso de las geométricas fraccionadas, los términos varían, en este caso de forma lineal (aumento/disminución constante), produciéndose la variación con una unidad de tiempo mayor que aquella en la que vienen los capitales, cualquiera que sea el tipo de interés de la renta (por ejemplo, variación anual y capitales semestrales; variación trimestral y capitales mensuales, …).
Las fórmulas de las rentas en aritmética sólo se pueden aplicar cuando los términos, el tanto de valoración y la razón de la renta están expresados en la misma unidad (obligatoriamente la de la razón, para que haya progresión).
Por tanto, las situaciones anteriores (y cualquier caso parecido) no se podrán resolver aplicando directamente las fórmulas de las rentas en progresión aritmética sin más.
Deberemos trabajar obligatoriamente en la unidad de tiempo en la que se produce la variación de los capitales (la unidad de la razón), lo que supondrá transformar, si es necesario, el tanto de valoración del problema (a través de la expresión de tantos equivalentes en compuesta). Por lo que se refiere a los capitales, éstos se mantienen constantes a nivel de subperíodo, dentro de cada período, y sólo varían de un período a otro y de la misma manera que se cambia el tipo de interés, se deberán sustituir los términos por otros equivalentes en la unidad de la razón de la progresión.
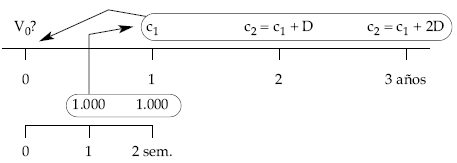
Para el caso de una renta variable en la que los términos aumentan periódicamente una cantidad d (progresión aritmética de razón d), con términos fraccionados, pospagables, temporal (de n períodos), al tanto i de valoración, la representación será la siguiente:
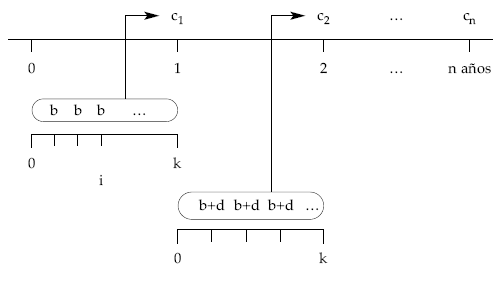
Calculando el primero de los términos equivalentes (c1):
el resto de términos equivalentes se obtienen a partir del primero, porque varían en progresión aritmética, siendo la razón el valor final de la renta que forma los aumentos constantes (d):
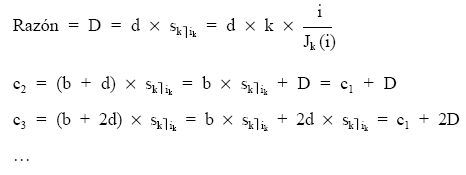
Trabajando en la unidad de variación de los capitales (la de la razón):
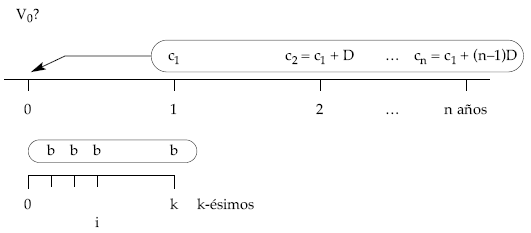
5.3.1. Valor actual
Si se quiere emplear una terminología en la que se aprecie el fraccionamiento, la expresión del valor actual queda así:
Siendo:
k: la frecuencia de fraccionamiento.
b x k:
la suma aritmética de los capitales del primer período de la renta.
d x k:
la suma aritmética de los aumentos de un período respecto a otro (razón de la progresión).
n: el número de períodos (en la unidad de tiempo de la razón).
i: el tipo de interés en la unidad de tiempo de la razón.
A partir del valor actual pospagable se puede obtener el resto de valores: prepagable, final, perpetuo, diferido y anticipado, sin más que tener las consideraciones ya comentadas para estos cálculos en cualquier tipo de renta.
5.3.2. Valor final
5.3.3. Prepagable
En las rentas prepagables, cuando se convierten en pospagables multiplicando por (1 + tipo de interés) habrá que hacerlo con el tanto en el que vienen los capitales (1 + ik).
5.3.4. Perpetua
EJEMPLO 17
Calcular el valor actual y final de la siguiente renta:
- Duración: 3 años.
- Términos semestrales vencidos de 1.000 euros durante el primer año.
- Aumento anual de los términos de un 10% sobre las cuantías del primero de ellos.
- Tanto de valoración del 8% efectivo anual.
Se trata de una renta variable en progresión aritmética (aumento de tipo lineal) por años, con términos semestrales vencidos (fraccionada), temporal e inmediata.
Gráficamente:
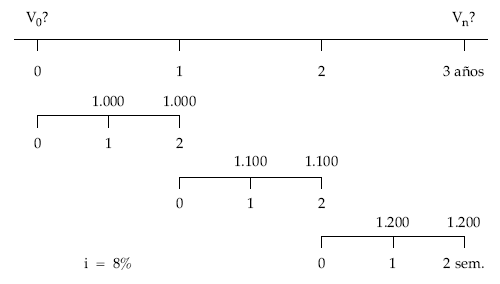
• Cálculo del valor actual empleando la terminología del fraccionamiento:
• Cálculo del valor actual empleando el término equivalente:
• Cálculo del valor final: