Será una renta continua todo conjunto de capitales separados entre sí por períodos infinitesimales. Parece, pues, que este tipo de rentas se pueden entender como rentas fraccionadas donde el fraccionamiento tiende a ser infinito dentro de cada período.
En la práctica se pueden considerar rentas continuas aquellas cuya frecuencia de fraccionamiento del término sea superior a 12.
6.1.
RENTA CONSTANTE, TEMPORAL, POSPAGABLE, INMEDIATA Y CONTINUA
Comenzaremos por la unitaria, tomando como referencia la unidad en la que viene expresado el tanto, y subdividiendo los períodos en infinitos subperíodos.
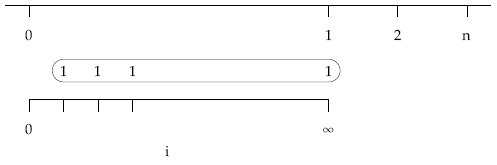
Si queremos calcular el valor actual de una renta unitaria, temporal, pospagable, inmediata y fraccionada, tendiendo este fraccionamiento a infinito (anù i), el desarrollo es el siguiente:
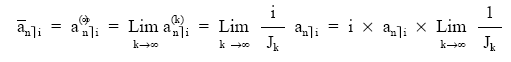
por otra parte:
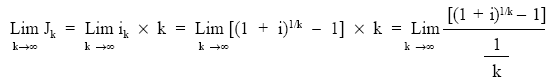
aplicando la regla de L’Hopital:
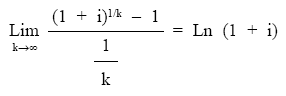
el resultado final es:
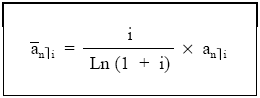
Cuando la renta es constante de cuantía c:
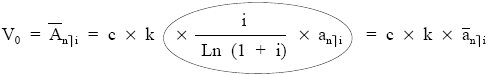
Iguales resultados se obtendrían si la renta se considera prepagable, puesto que al ser infinitesimal el subperíodo no hay diferencias entre el inicio y el final del mismo.
El cálculo del valor final se obtendría capitalizando el valor actual:
![]()
Las rentas perpetuas son aquellas cuya duración tiende a infinito. El valor actual de estas rentas se obtendrá con el concepto matemático del límite, cuando la duración de la renta tiende a infinito.
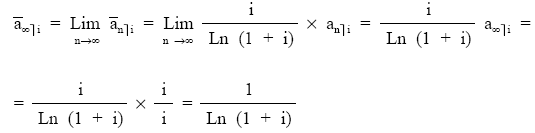
Cuando la renta es constante de cuantía c:
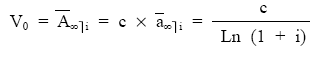
| Conclusión: las rentas continuas, a efectos de cálculo, se pueden considerar como una renta fraccionada con frecuencia de fraccionamiento superior a 12, pudiéndose aplicar todas las fórmulas de las rentas fraccionadas cambiando el Jk (i) por Ln (1 + i). |
EJEMPLO 18
Calcular el valor actual y final de la renta formada por los ingresos generados por una empresa sabiendo que éstos son de 100 euros diarios durante 5 años, siendo el tanto de valoración el 12% efectivo anual. Considérese año comercial.
Al venir los términos en una unidad de tiempo (días) inferior a la del tanto de valoración (año), se trata en principio de una renta fraccionada.
Pero, como además, la frecuencia de fraccionamiento es superior a 12, la trataremos como renta continua. Temporal de 5 años e inmediata.
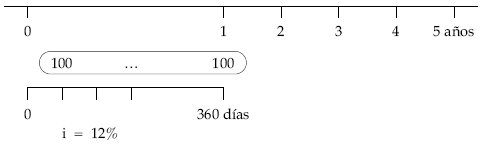
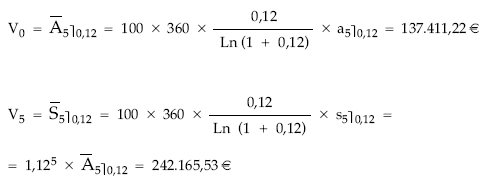
Si se hubiese resuelto como renta fraccionada, a través del tanto equivalente, en cuyo caso habría que calcular el tanto diario a partir del tanto anual de partida, el resultado sería el siguiente:
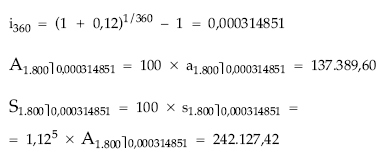
Como se puede apreciar, existen ciertas diferencias entre los resultados obtenidos por uno y otro sistema, debido a que al trabajar con el tanto equivalente no se ha tenido en cuenta la consideración del límite que las otras expresiones sí que llevan implícitas.
6.2. RENTA CONTINUA VARIABLE EN PROGRESIÓN GEOMÉTRICA
Se trata de una renta fraccionada en progresión geométrica con la particularidad de que ahora en lugar de haber un número finito de subperíodos consideraremos infinitos.
Considerándola temporal e inmediata, la representación gráfica será la siguiente:
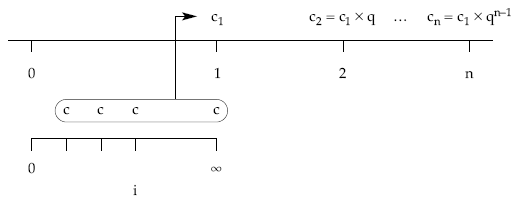
El valor actual de la renta, tanto pospagable como prepagable, quedará:
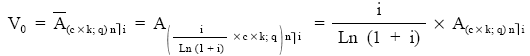
EJEMPLO 19
Calcular el valor actual y final de la renta formada por los ingresos de una persona, sabiendo que éstos son de 100 euros diarios durante 5 años, aumentando de manera acumulativa un 3% cada año, siendo el tanto de valoración el 12% efectivo anual. Considérese año comercial.
Al venir los términos en una unidad de tiempo (días) inferior a la del tanto de valoración (año), se trata, en principio, de una renta fraccionada. Pero, como además, la frecuencia de fraccionamiento es superior a 12, la trataremos como renta continua. Temporal de 5 años e inmediata.
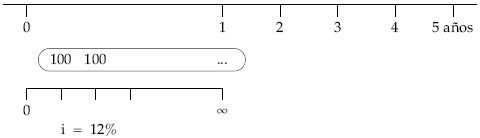
• Valor actual:
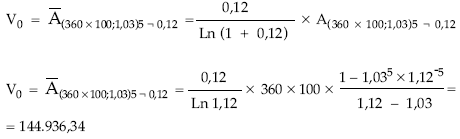
• Valor final:
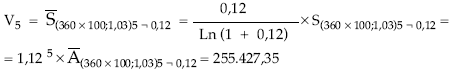
No obstante, se podría haber resuelto como renta fraccionada, a través del término anual equivalente:
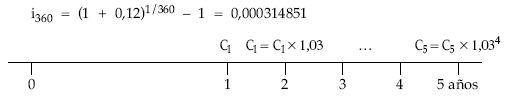

• Valor actual:
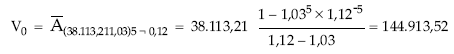
• Valor final:
![]()
Como se puede apreciar, al igual que en los ejemplos anteriores, existen ciertas diferencias entre los resultados obtenidos por uno y otro sistema.
A partir del valor actual pospagable se puede obtener el resto de valores: final, perpetuo, diferido y anticipado, sin más que tener las consideraciones ya comentadas para estos cálculos en cualquier tipo de renta.
6.3. RENTA CONTINUA VARIABLE EN PROGRESIÓN ARITMÉTICA
Se trata de una renta fraccionada en progresión aritmética, de razón d, con la particularidad de que ahora en lugar de haber un número finito de subperíodos consideraremos infinitos.
Partiendo de una renta temporal e inmediata, cuya representación gráfica es la que sigue, obtendremos el resto de posibles casos que nos podemos encontrar.
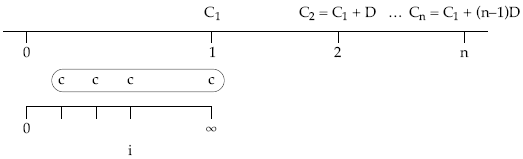
El valor actual de la renta, tanto pospagable como prepagable, quedará:
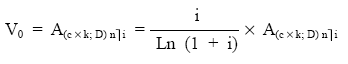
Siendo D la razón de la progresión aritmética:
![]()
A partir del valor actual pospagable se puede obtener el resto de valores: prepagable, final, perpetuo, diferido y anticipado.




