Las rentas de cuantía constante pueden, a su vez, subdividirse en unitarias o no unitarias, pospagables y prepagables, temporales o perpetuas, inmediatas, diferidas o anticipadas, enteras y fraccionadas. Iremos analizando cada uno de estos supuestos.
2.1.
RENTA CONSTANTE, UNITARIA, TEMPORAL, POSPAGABLE, INMEDIATA Y ENTERA
Vamos a estudiar una renta constante (términos de igual cuantía), temporal (tiene un número determinado de capitales), pospagable (los términos vencen al final del período), inmediata (valoraremos la renta en su origen y su final) y entera (términos y tanto están en la misma unidad de tiempo). Aunque no se diga expresamente se calculará en régimen de compuesta (renta compuesta).
2.1.1. Cálculo del valor actual
Comenzaremos por la renta constante más fácil, la que tiene como término la unidad (renta unitaria), cuya representación gráfica es la siguiente:
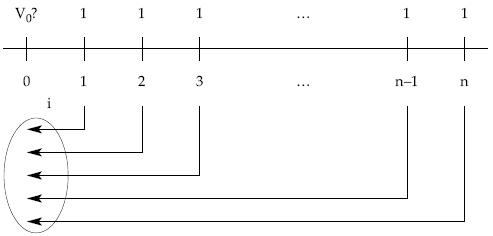
Aplicando la definición de valor actual y llevando los términos uno a uno, descontando en régimen de descuento compuesto al tanto de la renta i, desde donde están cada uno de los capitales hasta el origen se obtiene el valor actual, que se nota con la siguiente terminología anùi, donde n representa el número de capitales e i el tanto de valoración:
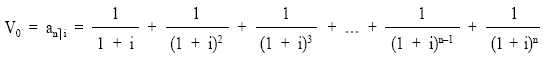
que supone la suma de n términos en progresión geométrica decreciente de razón:
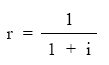
que se puede calcular con la siguiente expresión:
![]()
que permite sumar n términos en progresión decreciente, donde a1 es el primer término de la progresión, an es el último término y r es la razón.
Aplicando dicha fórmula a los términos actualizados de la renta y simplificando posteriormente:
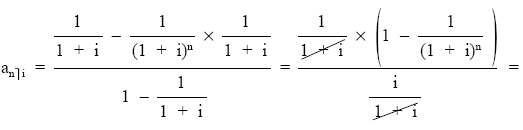
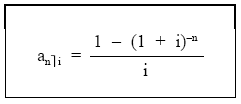
expresión que permite mover n capitales de una unidad monetaria equidistantes entre sí hasta su origen al tanto de interés i.
Sin embargo, el importe de los capitales no suele ser unitario. En el supuesto de encontrarnos con una renta constante cuyos términos fueran de cuantía c, el valor actual se representa por Anùi y se obtendría de la siguiente forma:
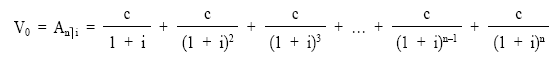
Sacando factor común el término c:
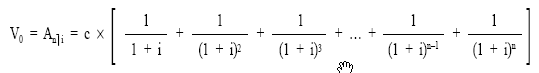
Donde el corchete es el valor actual de la renta unitaria, temporal, pospagable, inmediata y entera de n términos, anùi:
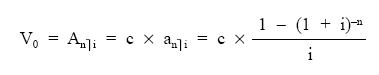
La expresión Anùi indica, pues, que la renta es constante de cuantía diferente de la unidad.
EJEMPLO 1
Calcular el valor actual de una renta de tres términos anuales vencidos de 100 euros cada uno a un tanto de interés del 10% efectivo anual.
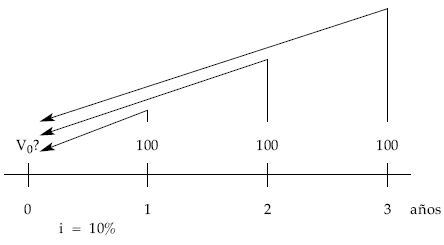
Moviendo los capitales uno a uno:
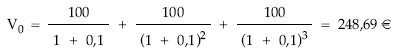
Utilizando la renta:
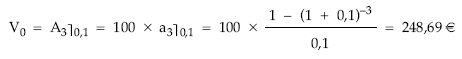
EJEMPLO 2
Calcular el valor de la imposición que tendremos que realizar en un banco que capitaliza al 12% de interés efectivo anual compuesto, si queremos disponer de 20.000 euros al final de cada uno de los próximos 5 años.
Las cantidades a recibir en el futuro constituyen una renta constante, temporal, pospagable, inmediata y entera. Por tanto, para que exista equivalencia entre la imposición y los reintegros, aquélla debe coincidir con el valor actualizado de estos últimos. Así, la imposición inicial será el valor actual de la renta formada por los reintegros al tanto que genera la operación.
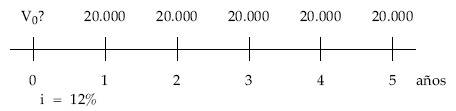
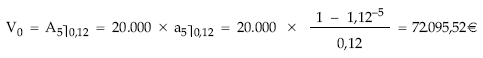
2.1.2. Cálculo del valor final
Seguimos trabajando con la misma renta constante, unitaria, temporal –n capitales–, pospagable, inmediata y entera; pero ahora vamos a calcular su valor final, es decir, valoraremos todos los términos de la renta en su final (momento n), quedando gráficamente así:
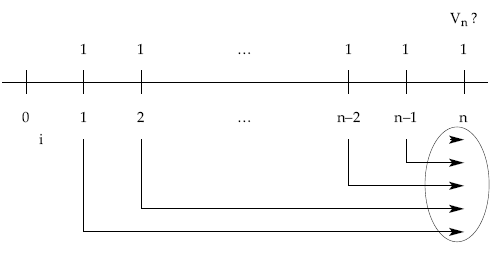
Aplicando la definición de valor final y llevando los términos uno a uno, capitalizando en régimen de capitalización compuesta al tanto de la renta i, desde donde se encuentra cada uno hasta el final, se obtiene el valor final, que se nota con la siguiente terminología snùi siendo n el número de capitales e i el tanto de valoración:
![]()
Que no es sino la suma de n términos en progresión geométrica creciente de razón r = 1 + i, que se puede calcular con la siguiente expresión:
![]()
donde a1 es el primer término de la progresión, an es el último término y r es la razón.
Aplicando dicha fórmula a los términos capitalizados de la renta y simplificando posteriormente queda:
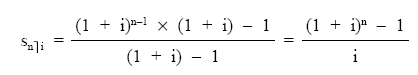
Al mismo resultado hubiésemos llegado si se capitaliza el valor actual de la renta hasta su final empleando el mismo tanto de valoración:
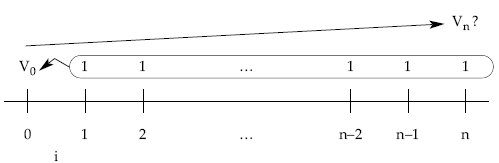
por tanto el valor final de la renta será la capitalización de su valor actual.
Comprobación:
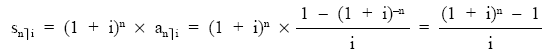
En el supuesto de ser los términos de cuantía c, el valor final (Snùi) se calculará así:
![]()
Simplificando, tomando factor común el término c:
![]()
Donde el corchete es el valor final de la renta unitaria, temporal de n términos, pospagable, inmediata y entera, snùi:
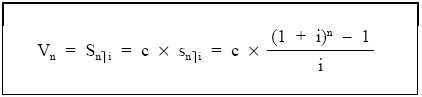
Y, de igual forma, se puede obtener capitalizando el valor actual:
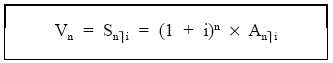
EJEMPLO 3
Calcular el valor final de una renta de tres términos anuales vencidos de 100 euros cada uno a un tanto de interés del 10% efectivo anual.
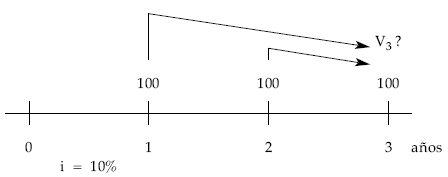
Desplazando los capitales uno a uno:
V3 = 100 x (1 + 0,1)2 + 100 x (1 + 0,1) + 100 = 331 €
Utilizando la renta:
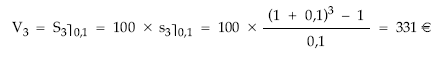
Capitalizando el valor actual:
V3 = 248,69 x (1 + 0,1)3 = 331 €
EJEMPLO 4
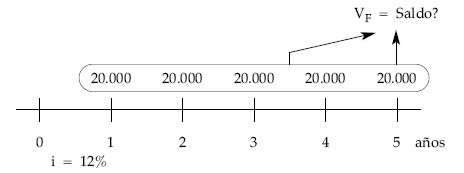
Calcular el importe acumulado en un banco al cabo de 5 años, si imponemos al final de cada uno de ellos 20.000 euros siendo el tipo de interés de la cuenta el 12% efectivo anual.
El importe acumulado después de 5 años será el valor final de la renta formada por las imposiciones que se han realizado, utilizando como tanto de valoración el tipo de interés de la propia cuenta.
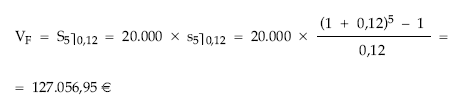
EJEMPLO 5
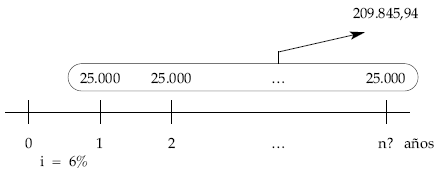
Calcular el número de ingresos de 25.000 euros que tenemos que realizar al final de cada año para reunir 209.845,94 euros en un banco que capitaliza al 6% efectivo anual.
En este caso se conoce la cuantía a imponer periódicamente, que constituye una renta constante, y el saldo que queremos tener constituido (el valor final de la renta); lo que se desea conocer es el número de imposiciones a realizar, esto es, el número de términos de la renta (n) que constituyen las imposiciones.
![]()
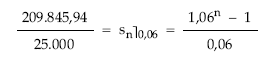
y mediante logaritmos se despeja la incógnita n:
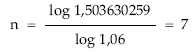
2.2. RENTAS PREPAGABLES
Vamos a estudiar una renta constante (términos de igual cuantía), temporal (tiene un número determinado de capitales), prepagable (los términos vencen al principio del período), inmediata (valoraremos la renta en su origen y su final) y entera (términos y tipo de interés están en la misma unidad de tiempo). Aunque no se diga expresamente se calculará en régimen de compuesta (renta compuesta).
2.2.1. Cálculo del valor actual
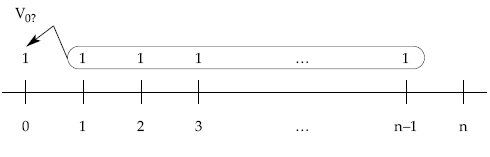
Comenzaremos por la renta constante que tiene como término la unidad (renta unitaria), cuya representación gráfica es la siguiente:
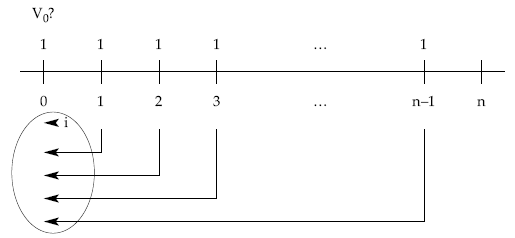
Aplicando la definición de valor actual y llevando los términos uno a uno, descontando en régimen de descuento compuesto al tanto de la renta i, desde donde está cada capital hasta el origen se obtiene el valor actual que notaremos por änùi:
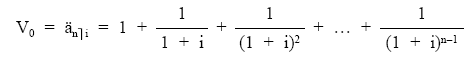
que supone la suma de n términos en progresión geométrica decreciente de razón:
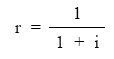
que se puede calcular con la siguiente expresión:
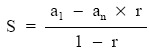
Aplicando dicha fórmula a los términos actualizados de la renta y simplificando posteriormente:
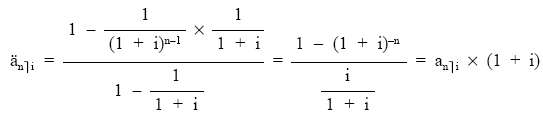
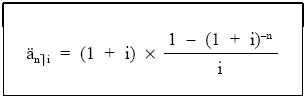
expresión que permite mover n capitales de una unidad monetaria equidistantes entre sí hasta su origen, al tanto de interés i.
Otra posibilidad consiste en calcular el valor actual de la renta prepagable valorando por separado el primer capital, que ya está en el origen, y el resto de capitales (n – 1) como renta pospagable inmediata:
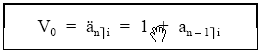
Para rentas constantes cuyos términos fueran de cuantía c, el valor actual (Änùi) se obtiene valorando en el origen cada uno de esos capitales:
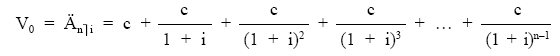
Sacando factor común c:
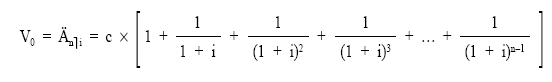
Donde el corchete es el valor actual de la renta unitaria, temporal, prepagable, inmediata y entera, änùi:
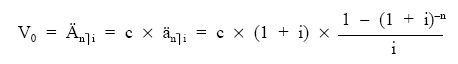
La expresión Änùi indica que la renta es constante de cuantía diferente de la unidad.
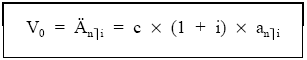
| Nota: los valores actuales y finales de las rentas prepagables se obtienen a partir de las rentas pospagables multiplicando por (1 + i), es decir, las rentas prepagables son el resultado de capitalizar un período las rentas pospagables. |
EJEMPLO 6
Calcular el valor actual y final de una renta de tres términos anuales situados a principios del año de 100 euros cada uno a un tanto de interés del 10% efectivo anual.
• Valor actual
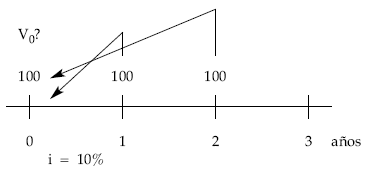
Moviendo los capitales uno a uno:
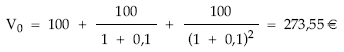
Utilizando la renta:
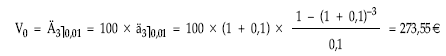
• Valor final
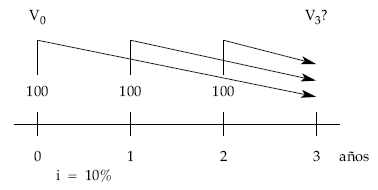
Moviendo los capitales uno a uno:
V3 = 100 x (1 + 0,1)3 + 100 x (1 + 0,1)2 + 100 x (1 + 0,1) = 364,10 €
Utilizando la renta:
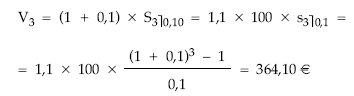
Capitalizando el valor actual:
V3 = 273,55 x (1 + 0,1)3 = 364,10 €
2.3. RENTAS PERPETUAS
Las rentas perpetuas son aquellas cuyo número de términos es infinito. Por este motivo a este tipo de rentas sólo se le podrá calcular valor actual pero nunca el valor final, y todo ello con independencia de que sea pospagable o prepagable, constante o variable, etc.
El valor actual de estas rentas se obtendrá viendo qué ocurre si aplicamos las fórmulas empleadas para rentas temporales y en lugar de utilizar un número finito de capitales (n) trabajamos con infinitos términos (∞∞). En definitiva, se trata de trabajar con el concepto matemático de los límites, cuando la duración de la renta (y por tanto, el número de capitales) tiende a infinito.
En el caso de renta constante, pospagable, inmediata y entera:
• Renta unitaria:
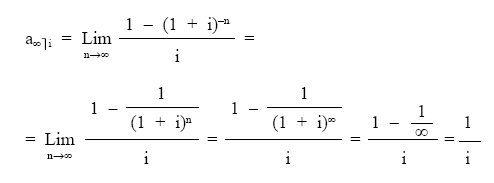
• Renta no unitaria:
Será la cuantía del término multiplicado por la renta unitaria:
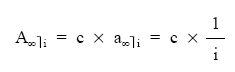
En el caso de una renta constante, prepagable, inmediata y entera, se puede hacer uso de la definición de renta perpetua, pero también se puede hacer uso de la regla habitual de calcular la renta prepagable multiplicando por (1 + i) la misma renta considerada pospagable.
• Renta unitaria:
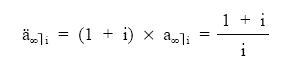
• Renta no unitaria:
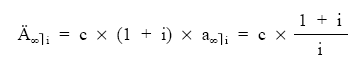
Hallar el valor actual de una renta perpetua semestral con un término de 25.000 euros si el tanto de valoración es el 12% nominal capitalizable por semestres, en los siguientes casos:
a) Si los capitales son pospagables.
b) Si los capitales son prepagables.
![]()
a) Pospagables:
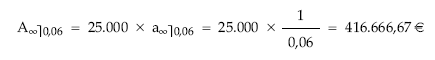
b) Prepagables:
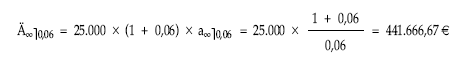
2.4. RENTAS DIFERIDAS
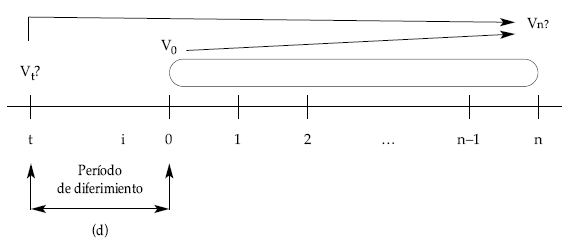
Son aquellas que se valoran con anterioridad a su origen. El tiempo que transcurre entre el origen de la renta y el momento de valoración se denomina período de diferimiento de la renta.
Si partimos de una renta unitaria, temporal (de n términos) y pospagable se trata de valorar los capitales directamente, uno a uno, en el momento de valoración elegido.
Gráficamente quedaría:
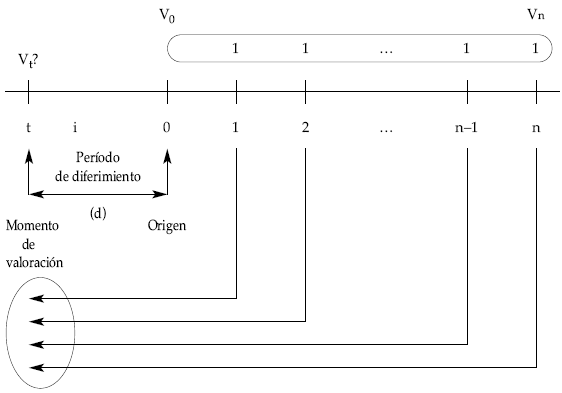
Al aplicar la definición de valor financiero en el momento t:
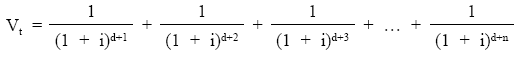
Sacando factor común:
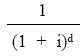
quedará:
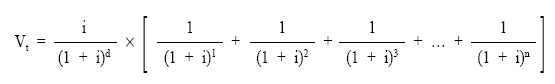
Donde el corchete representa el valor actual de la renta unitaria, temporal (n términos), pospagable, inmediata y entera (anùi), que posteriormente se descuenta como un capital único, al mismo tipo (i), durante el período de diferimiento (d). Por tanto, se obtendría el mismo resultado si valoramos la renta en su origen (se considera como inmediata y se calcula su valor actual) y posteriormente se descuenta dicho valor actual (como un solo capital) hasta el momento t elegido, en régimen de descuento compuesto al tanto de interés vigente durante el período de diferimiento. Gráficamente sería:
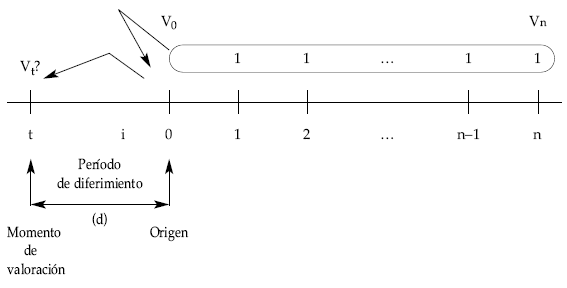
Analíticamente quedaría así:
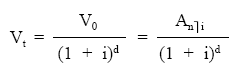
Expresión esta que puede notarse de forma abreviada de la siguiente forma: d/anùi, donde n representa el número de términos de la renta, i, el tanto de valoración y d, el período de diferimiento.
Si la renta fuera constante, pero de cuantía diferente de la unidad (no unitaria) todo lo dicho seguiría siendo válido y bastaría con multiplicar el valor de la renta unitaria por la cuantía del término.
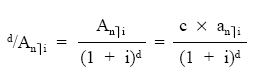
El diferimiento solamente afecta al valor actual, por tanto, si lo que se quiere calcular es el valor final de la renta, aplicando la definición de valor final se ratará como una renta inmediata, aunque también se podría obtener dicho valor final a partir del valor actual diferido:
Vn = V0 x (1 + i)n = Vt x (1 + i)d+n
EJEMPLO 8
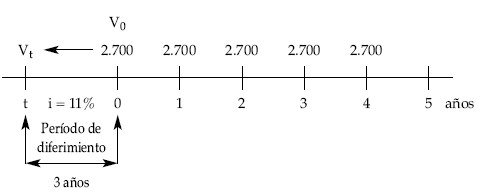
Calcular el valor actual y final de una renta cuya duración es de 5 años, con términos anuales prepagables de 2.700 euros sabiendo que se empiezan a devengar dentro de 3 años. Tanto de valoración 11% efectivo anual.
Se trata de una renta diferida 3 años, con términos prepagables y 5 términos.
• Valor actual:
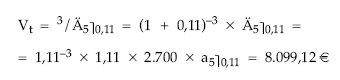
• Valor final:
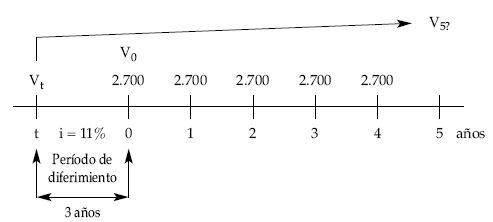
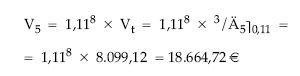
El diferimiento no afecta al valor final, que se podía haber calculado como el de una renta inmediata de 5 términos prepagables:
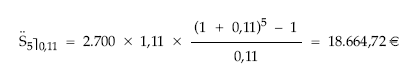
2.5. RENTAS ANTICIPADAS
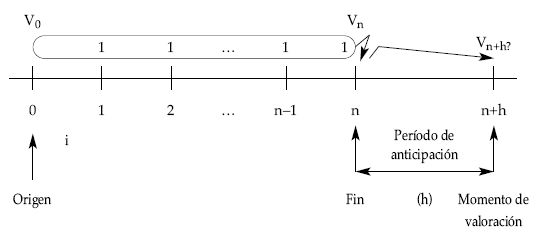
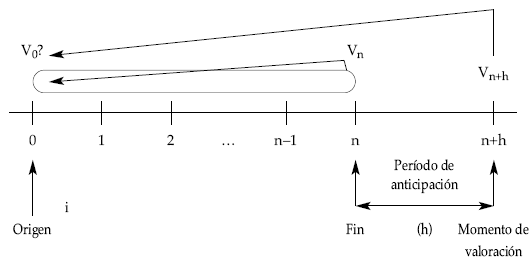
Son aquellas que se valoran con posterioridad a su final. El tiempo que transcurre entre el final de la renta y el momento de valoración se denomina período de anticipación de la renta.
Si partimos de una renta unitaria, temporal (de n términos) y pospagable se trata de valorar los capitales directamente, uno a uno, en el momento de valoración elegido.
Gráficamente quedaría:
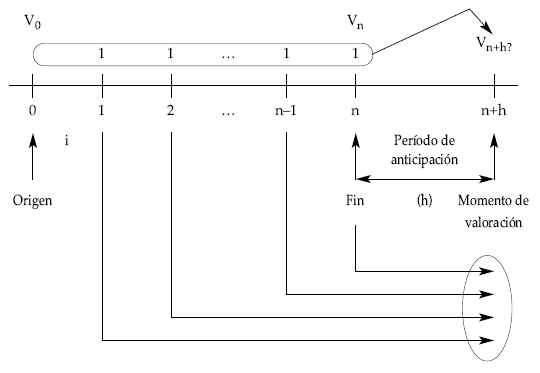
Al aplicar la definición de valor financiero en el momento t:
Vn+h = (1 + i)h + (1 + i)h+1 + (1 + i)h+2 + … + (1 + i) h+n-1
Sacando factor común (1 + i)h quedará lo siguiente:
Vn+h = (1 + i)h x [1 + (1 + i) + (1 + i)2 + … + (1 + i)n-1]
Donde el corchete representa el valor final de la renta unitaria, temporal (n términos), pospagable, inmediata y entera (snùi), que posteriormente se capitaliza como un capital único, al mismo tipo (i), durante el período de anticipación (h). Por tanto, si primero se valora la renta en su final y posteriormente capitalizamos el valor final, como un solo capital, se obtendría el mismo resultado.
Analíticamente quedaría así:
![]()
Expresión esta que puede notarse de forma abreviada de la siguiente forma: h/s nùi, donde n representa el número de términos de la renta, i, el tanto de valoración y h, el período de anticipación.
La anticipación solamente afecta al valor final pero no al valor actual, que se realizará como si de una renta inmediata se tratara, cumpliéndose la siguiente relación entre diferentes valores de la renta:
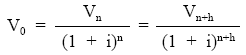
Todo lo anterior se cumple, de igual forma, para rentas constantes de cuantía diferente a la unidad (no unitarias).
EJEMPLO 9
Calcular el valor actual y final de una renta de 3 términos anuales de 1.000 euros pagaderos por vencido si la valoración al 7% anual se efectúa a los 8 años de comenzada la renta.
Se trata de una renta anticipada, puesto que la valoración se realiza 5 años después de haberse hecho efectivo el último capital. No obstante, la anticipación no afecta al valor actual que se resolverá como una renta inmediata.
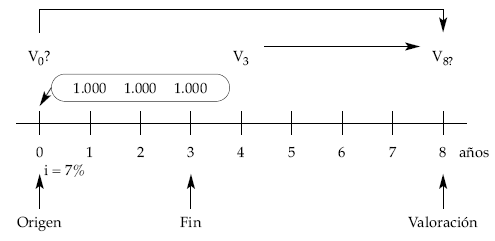
• Valor actual:
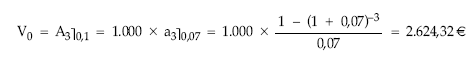
• Valor final:
![]()
también:
V8 = V0 x (1 + 0,07)8 = 2.624,32 x (1 + 0,07)8 = 4.509,06 €




