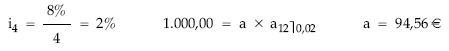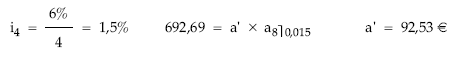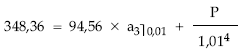Los préstamos se pueden clasificar atendiendo al interés aplicable durante toda la vida del préstamo, pudiéndose distinguir los siguientes tipos:
a)Préstamos tipo fijo.
El tipo de interés aplicable durante toda la vida de la operación se mantiene constante y se fija en el momento de contratación.
b) Préstamos tipo variable (revisable).
El tipo de interés aplicable en la operación se obtiene tomando como base un índice (tipo referencial) al que se suma un diferencial constante. El tipo de interés se ajustará periódicamente en función del comportamiento de la referencia tomada como base. Las referencias más utilizadas publicadas por el Banco de España son:
- Índice de referencia de préstamos hipotecarios de los bancos.
- Índice de referencia de préstamos hipotecarios de las cajas de ahorros.
- Índice de referencia de préstamos hipotecarios del conjunto de entidades.
- Índice CECA.
- Deuda Pública
- Euribor a un año.
c) Préstamos tipo mixto.
Funcionan como un préstamo a tipo fijo durante un determinado período de tiempo y posteriormente se convierten en un préstamo de interés variable durante el resto de la vida de la operación.
En las operaciones de amortización con tipos de interés mixto o variable, en el momento de la contratación no se conocen los tipos de interés a aplicar durante los diferentes períodos que dura la operación. En dicho momento se pacta el importe prestado, la duración de la operación, el tipo de interés a aplicar durante el primer período (denominado tipo de interés de salida), el tipo de interés de referencia, en base al cual se va modificando el tipo de interés de los restantes períodos y el diferencial a añadir al tipo de referencia.
El período de revisión del tipo de interés puede ser trimestral, semestral, anual, etc.
Para la revisión de los tipos de interés existen diferentes alternativas, que determinarán la estructura definitiva de los pagos efectuados y, en consecuencia, la estructura del cuadro de amortización:
- Recalculando la cuantía de los términos amortizativos.
- Manteniendo constante la cuantía de los términos amortizativos y modificando el número de pagos a realizar: sistema de cuota fija.
- Manteniendo el plan de amortización inicial: plan de amortización sin cambios.
14.1. RECÁLCULO DEL TÉRMINO AMORTIZATIVO
En este caso para cada revisión del tipo de interés se calcula el término a pagar como una nueva operación de amortización, donde el importe del capital será el capital vivo en ese momento; la duración de la operación, la vida remanente del préstamo; y el tipo de interés, el vigente en ese momento y aplicándolo para el resto de la operación.
Así, se modificará el término amortizativo cada vez que haya una revisión del tipo de interés, cambiando asimismo su composición.
14.2. MANTENIMIENTO DEL IMPORTE DEL TÉRMINO AMORTIZATIVO SIN CAMBIOS
El término amortizativo inicialmente calculado se va a mantener durante todo el préstamo. En cada revisión del tipo de interés se plantea el préstamo como una nueva operación donde el importe del capital será el capital vivo en ese momento; el tipo de interés, el vigente en ese momento y aplicándolo hasta el final; como término amortizativo se mantiene el que se calculó inicialmente; por último, se calcula el número de pagos a realizar en esa situación para la completa amortización del capital pendiente.
De esta forma el importe de los pagos se mantiene sin cambios en su cuantía total, pero la modificación del tipo de interés supondrá una nueva variación en la composición del termino, de forma que una subida de tipo de interés se traduce en una mayor cuota de interés y menor cantidad destinada a amortización (al revés, si se produce una rebaja de tipos).
En esta modalidad de revisión de los tipos de interés lo que nunca se conocerá (hasta la última revisión) es el número de pagos constantes que se realizarán en total. Si los tipos van disminuyendo, se acortará el número de pagos, y aumentará cuando los tipos de interés futuros vayan creciendo.
14.3. PLAN DE AMORTIZACIÓN SIN CAMBIOS
Cuando se establece el plan de amortización fijo lo que se determina en el momento de la contratación es el capital prestado, la duración del préstamo, el tipo de interés de salida y las cuotas de amortización de cada período, que una vez establecidas serán inamovibles. En cada uno de los períodos de revisión del tipo de interés bastará con añadir a la cuota de amortización la nueva cuota de interés. Esta última se calculará, como en cualquier caso, como el producto del capital vivo por el tipo de interés aplicable en cada período, una vez revisado.
Al permanecer sin cambios las cuotas de amortización calculadas para todos y cada uno de los períodos, y variar solamente las cuotas de interés como consecuencia de la revisión de tipos, los términos amortizativos (ak) se volverán aleatorios.
EJEMPLO 19
Se contrata un préstamo en las siguientes condiciones:
- Importe: 1.000 euros.
- Duración: 3 años.
- Términos amortizativos trimestrales constantes.
- Tipo de interés nominal durante el primer año del 8%.
- Para el resto de años, EURIBOR + 1%, con revisiones anuales.
Supondremos que en la primera revisión dicho tipo será del 5% y en la segunda, el 3%.
Se pide:
- Cuadro de amortización inicial.
- Cuadro resultante después de las revisiones previstas en los siguientes casos:
– Recalculando el término amortizativo.
– Manteniendo el importe del término sin cambios.
– Plan de amortización sin cambios.
Cuadro de amortización inicial
Se trata de un préstamo tipo francés, con término amortizativo constante y considerando como tipo de interés para toda la operación (12 trimestres) el que se aplica durante el primer año (8% nominal), es decir, se calcula bajo el supuesto teórico de que el tipo inicial permanece constante durante toda la vida del préstamo.
|
Número pago
|
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
0
1 2 3 4 |
0,02
0,02 0,02 0,02 |
94,56
94,56 94,56 94,56 |
20,00
18,51 16,99 15,44 |
74,56
76,05 77,57 79,12 |
74,56
150,61 228,18 307,31 |
1.000,00
925,44 849,39 771,82 692,69 |
|
5
6 7 8 |
0,02
0,02 0,02 0,02 |
94,56
94,56 94,56 94,56 |
13,85
12,24 10,59 8,91 |
80,71
82,32 83,97 85,65 |
388,01
470,33 554,30 639,95 |
611,99
529,67 445,70 360,05 |
|
9
10 11 12 |
0,02
0,02 0,02 0,02 |
94,56
94,56 94,56 94,56 |
7,20
5,45 3,67 1,85 |
87,36
89,11 90,89 92,70 |
727,31
816,41 907,30 1.000,00 |
272,70
183,59 92,70 |
|
Total
|
|
1.134,72
|
134,72
|
1.000,00
|
|
|
Revisión del tipo mediante el sistema del recálculo del término amortizativo
Para construir el cuadro definitivo partimos del cuadro inicial, que se va a mantener sin cambios hasta pasado un año, fecha de la primera revisión del tipo de interés.
|
Número pago
|
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
0
1 2 3 4 |
0,02
0,02 0,02 0,02 |
94,56
94,56 94,56 94,56 |
20,00
18,51 16,99 15,44 |
74,56
76,05 77,57 79,12 |
74,56
150,61 228,18 307,31 |
1.000,00
925,44 849,39 771,82 692,69 |
Realizado el cuarto pago, la deuda pendiente (692,69 euros) se tomará como importe de un nuevo préstamo, de duración los dos años –que aún faltan para concluir definitivamente el préstamo–, y empleando como tipo el que surja como consecuencia de la revisión (un nominal del 6%), con el mismo sistema de amortización (francés) y se «recalcula» el término amortizativo. Se obtiene una nueva trimestralidad (92,53 euros), con una nueva distribución entre interés y principal, vigentes hasta la nueva revisión.
|
Número pago
|
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
5
6 7 8 |
0,015
0,015 0,015 0,015 |
92,53 |
10,39
9,16 7,91 6,64 |
82,14
83,38 84,63 85,90 |
389,45
472,83 557,45 643,35 |
610,55
527,18 442,55 356,66 |
Pasados dos años (ocho pagos trimestrales), momento de la segunda revisión del tipo de interés, se vuelve a realizar la operación efectuada en la primera revisión. En este caso, el importe a considerar será la deuda pendiente en esa fecha (356,66 euros), duración un año y como tipo el 4% nominal aplicable en ese momento.
|
Número pago
|
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
9
10 11 12 |
0,01
0,01 0,01 0,01 |
91,40
91,40 91,40 91,40 |
3,57
2,69 1,80 0,91 |
87,84
88,72 89,60 90,50 |
731,18
819,90 909,50 1.000,00 |
268,82
180,10 90,50 |
Revisión del tipo mediante manteniendo el término amortizativo inicial sin cambios
También se parte del cuadro de amortización inicial calculado con un tipo único (8% nominal) para los tres años, que se va a mantener sin cambios hasta pasado un año, fecha de la primera revisión del tipo de interés.
|
Número pago
|
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
0
1 2 3 4 |
0,02
0,02 0,02 0,02 |
94,56
94,56 94,56 94,56 |
20,00
18,51 16,99 15,44 |
74,56
76,05 77,57 79,12 |
74,56
150,61 228,18 307,31 |
1.000,00
925,44 849,39 771,82 692,69 |
En el momento de la primera revisión, aunque el tipo de interés cambie, se mantiene sin variación el importe del término amortizativo inicialmente calculado (94,56 euros). Se planteará un nuevo préstamo cuyo importe será la deuda aun pendiente (692,69 euros), con un nuevo tipo de interés –el vigente en esa fecha, 6% nominal–, siendo la incógnita el número de pagos a efectuar. Y es que en este sistema, el número de pagos definitivos no se conocerá hasta la última revisión de tipos.
Al variar el tipo de interés se produce una nueva distribución de término amortizativo en interés y principal.
|
Número pago
|
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
5
6 7 8 |
0,015
0,015 0,015 0,015 |
94,56
94,56 94,56 94,56 |
10,39
9,13 7,85 6,55 |
84,17
85,43 86,71 88,01 |
391,48
476,91 563,62 651,64 |
608,52
523,09 436,38 348,36 |
Pasados dos años, llega el momento de la segunda revisión del tipo de interés. Se vuelve a realizar la operación efectuada en la primera revisión. En este caso, el importe a considerar será la deuda pendiente en esa fecha (348,36 euros), el término 94,56 euros y como tipo el 4% nominal vigente en ese momento. Es en esta última revisión donde se obtendrá el número de pagos que teóricamente habrá que realizar para concluir la operación. El cálculo será el siguiente:
de donde:
Y, aunque la duración del préstamo no se ha visto disminuida a pesar del descenso de tipos, el importe del último pago será inferior al resto (como consecuencia del descenso de tipos). Su cuantía se obtendrá de la siguiente equivalencia en la fecha de la última revisión del tanto:
de donde:
P = 73,11 €
|
Número pago
|
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
9
10 11 12 |
0,01
0,01 0,01 0,01 |
94,56
94,56 94,56 73,11 |
3,48
2,57 1,65 0,72 |
91,08
91,99 92,91 72,39 |
742,71
834,70 927,61 1.000,00 |
257,29
165,30 72,39 |
Revisión del tipo mediante manteniendo las cuotas de amortización sin cambios (con respecto al cuadro inicial)
Se toma como punto de partida el cuadro inicial calculado al principio para los tres años de duración del préstamo. Dicho cuadro permanecerá sin cambios, a pesar de las revisiones de tipos, por lo que se refiere a las columnas de cuota de amortización, total amortizado y capital vivo.
A medida que se vaya modificando el tipo a aplicar en cada período, se calcularán las diferentes cuotas de interés. Para el cálculo de los términos amortizativos, bastará con sumar la cuota de interés (que cada trimestre se calcula al tipo nominal vigente en ese período) y la cuota de amortización (la calculada en el cuadro inicial para toda la operación) de cada uno de los trimestres.
|
Número
pago |
Tipo interés
|
Términos amortizativos
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
0
1 2 3 4 |
0,02
0,02 0,02 0,02 |
94,56
94,56 94,56 94,56 |
20,00
18,51 16,99 15,44 |
74,56
76,05 77,57 79,12 |
74,56
150,61 228,18 307,31 |
1.000,00
925,44 849,39 771,82 692,69 |
|
5
6 7 8 |
0,015
0,015 0,015 0,015 |
91,10
91,50 91,92 92,34 |
10,39
9,18 7,95 6,69 |
80,71
82,32 83,97 85,65 |
388,01
470,33 554,30 639,95 |
611,99
529,67 445,70 360,05 |
|
9
10 11 12 |
0,01
0,01 0,01 0,01 |
90,96
91,84 92,73 93,63 |
3,60
2,73 1,84 0,93 |
87,36
89,11 90,89 92,70 |
727,31
816,41 907,30 1.000,00 |
272,70
183,59 92,70 |
La ventaja de este sistema es la facilidad para construir el cuadro ya que desde el principio se conocen las cantidades destinadas a amortizar capital y, por tanto, los capitales pendientes. El importe de los términos amortizativos, no obstante, no puede conocerse de antemano, dado que no se conocen los tipos de interés que van a estar vigentes en futuros períodos, siendo diferentes todos ellos, desde el momento de la primera revisión del tipo de interés.