Este método se caracteriza porque:
- Los términos amortizativos varían en progresión geométrica, y
- El tanto de valoración y la razón de la progresión permanecen constantes, durante toda la operación.
De esta razón va a depender la variación que se irá produciendo en las cuotas. Así, a mayor razón menor es la cuota inicial y mayor será la final.
Además se pone de manifiesto que cuanto mayor es la razón de la progresión mayor es el importe de los intereses pagados a lo largo de toda la operación.
Gráficamente, el esquema de cobros y pagos de la operación para un préstamo de C0, a amortizar en n períodos, con pagos que varían en progresión geométrica de razón conocida q, al tipo de interés i, es el siguiente:
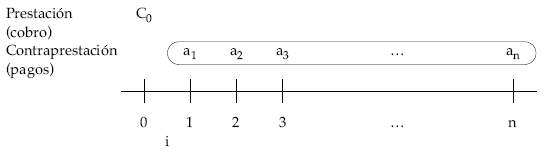
6.1. PASOS A SEGUIR
6.1.1. Cálculo de los términos amortizativos (ak)
Los pagos que se realizan durante la vida del préstamo incorporan la cuota de interés y la cuota de amortización. Para eliminar los intereses bastaría con actualizar los términos amortizativos a la tasa de interés del préstamo, con lo cual sólo quedarían las cuotas de principal, que sumadas coinciden con el importe del préstamo.
Es decir, planteamos una equivalencia financiera en el origen entre el importe del préstamo y la renta en progresión geométrica formada por los términos amortizativos, cuyo valor actual se pondrá en función del primer término y la razón de la progresión.
Al desarrollar esta equivalencia pueden darse dos casos según la relación entre la razón de la progresión que siguen los términos y el tipo de interés del préstamo:
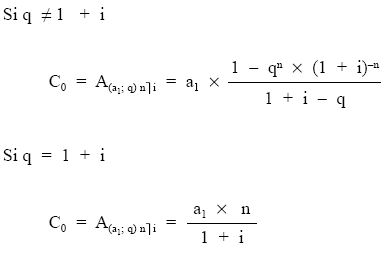
En ambos casos la variable desconocida y que se despeja es el primer término amortizativo (a1), que será la incógnita a calcular.
Una vez calculado el primer término amortizativo, al seguir los demás una progresión geométrica, el resto de ellos se calculará a través de dicha ley, así:
a2 = a1 x q
a3 = a2 x q = a1 x q2
…
ak+1 = ak x q = a1 x qk
…
an = an-1 x q = a1 x qn-1
6.1.2. Cálculo de las cuotas de amortización (Ak)
6.1.2.1. 1.ª posibilidad: a través de la estructura del término amortizativo
Una vez calculados los términos amortizativos, se cumple lo siguiente:
Período 1: a1 = I1 + A1 = C0 x i + A1, de donde se despeja A1 (ya que lo demás se conoce)
Período 2: a2 = I2 + A2 = C1 x i + A2 = (C0 – A1) x i + A2, y despejamos A2,
Período 3: a3 = I3 + A3 = C2 x i + A3 = (C1 – A2) x i + A3, y despejamos A3,
y así se continuaría hasta calcular el resto de cuotas de amortización.
6.1.2.2.
2.ª posibilidad: a través de la ley de recurrencia que siguen las cuotas de amortización
Al ser variable el término amortizativo, las cuotas de amortización normalmente también variarán, si bien el sentido de esta variación (creciente o decreciente) estará en función de la razón de la progresión y el tipo de interés del préstamo. No obstante, se puede comprobar si lo hacen siguiendo alguna ley matemática (ley de recurrencia).
Se trata de encontrar la relación matemática que siguen dos cuotas de amortización consecutivas. Para ello se relacionan por diferencias los términos amortizativos de dos períodos consecutivos cualesquiera:
Período k: ak = Ik + Ak = Ck-1 x i + Ak
Período k+1: ak+1 = Ik+1 + Ak+1 = Ck x i + Ak+1
——————————————————————
ak – ak+1 = (Ck-1 – Ck) x i + Ak – Ak+1
siendo: Ck-1 – Ck = Ak, queda:
ak – ak+1 = Ak x i + Ak – Ak+1
de donde:
Ak+1 = Ak x (1 + i) + ak+1 – ak
y como: ak+1 = ak x q, la expresión puede quedar:
Ak+1 = Ak x (1 + i) – ak x (1 – q)
expresión que permite calcular una cuota de amortización a partir de la cuota de amortización anterior.
Ley que puede resultar poco práctica, ya que además de conocer la cuota de amortización anterior se debe considerar el término amortizativo de aquel período, por lo que quizá sea más práctico hacer uso del primer sistema de cálculo anteriormente comentado.
6.1.3. Cálculo del total amortizado después de k períodos (mk)
Conocer la totalidad de la deuda amortizada en un momento de tiempo concreto se puede hacer de dos formas posibles:
• Por diferencias, entre el importe del préstamo y lo que aún se debe:
mk = C0 – Ck
• Por sumas de cuotas de amortización practicadas hasta la fecha:
mk = A1 + A2 + …. + Ak
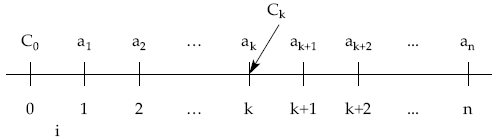
6.1.4. Cálculo del capital vivo a principios del período k+1 (Ck)
En este tipo de préstamos el cálculo del capital vivo a través de las cuotas de amortización resulta poco práctico, salvo que nos encontremos muy cerca del principio o del final de la operación. Pretendemos buscar un sistema que permita calcular el capital pendiente a partir de los términos amortizativos del préstamo.
Al trabajar con los términos amortizativos se deberán hacer de forma financiera (no bastará con sumar y restar aritméticamente) puesto que los términos incorporan intereses y principal; habrá que mover financieramente las cantidades correspondientes.
6.1.4.1.
1.ª posibilidad: método retrospectivo, a través de los términos amortizativos pasados
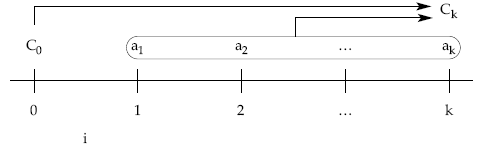
en k se debe cumplir:
lo que se debe en k = [lo recibido – lo pagado]k
por tanto en k:
![]()
6.1.4.2. 2ª posibilidad: método prospectivo, a través de los términos amortizativos futuros
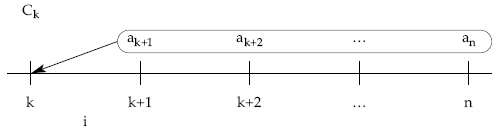
en k se debe cumplir:
lo que supondría la cancelación total en k = [cantidades pendientes de pagar]k
por tanto en k:
![]()
6.1.5. Cálculo de la cuota de interés del período k+1 (Ik+1)
Los intereses de cualquier período se calcularán a partir de la deuda pendiente a principios de ese período, al tanto efectivo vigente durante el mismo.
Ik+1 = Ck x i
EJEMPLO 6
Construir el cuadro de amortización de un préstamo de 10.000 euros, al 10% de interés anual, amortizable en 3 años, con anualidades que van aumentando un 5% cada año de forma acumulativa.
|
|
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
|
Años
|
Término amortizativo
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital
vivo |
|
0
1 2 3 |
3.838,50
4.030,43 4.231,94 |
1.000,00
716,15 384,72 |
2.838,50
3.314,28 3.847,22 |
2.838,50
6.152,78 10.000,00 |
10.000,00
7.161,50 3.847,22 |
|
Total
|
12.100,87
|
2.100,87
|
10.000,00
|
|
|
Descripción de los pasos a seguir para construir el cuadro:
(1) Se calcula el importe del pago total a realizar en el primer período (término amortizativo) a través de la fórmula anterior.
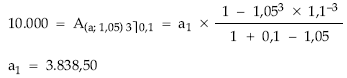
(2) La cuota de interés se calcula sobre el capital pendiente a principios de cada período (5).
(3) La cantidad destinada a amortizar será la diferencia entre el total pagado en el período (1) y lo que se dedica a intereses (2).
(4) Se calcula el total amortizado por sumas parciales de las cuotas de amortización practicadas hasta la fecha.
(5) La deuda pendiente se obtendrá de restar al capital a principios de cada período la cuota de amortización de ese mismo período, o bien, al importe del préstamo (C0) se le resta el total amortizado (4) ya acumulado hasta ese momento.




