Para comprobar si dos o más capitales resultan indiferentes (equivalentes) deben tener el mismo valor en el momento en que se comparan: principio de equivalencia de capitales.
El principio de equivalencia financiera nos permite determinar si dos o más capitales situados en distintos momentos resultan indiferentes o, por el contrario, hay preferencia por uno de ellos.
Ya vimos en las operaciones en simple la definición y utilidad de la equivalencia de capitales. El principio de equivalencia de capitales y sus aplicaciones siguen siendo válidos. La diferencia fundamental viene dada porque en régimen de compuesta la fecha donde se realice la equivalencia no afecta al resultado final de la operación, por tanto, si la equivalencia se cumple en un momento dado, se cumple en cualquier punto y, si no se cumple en un momento determinado, no se cumple nunca.
5.1. APLICACIONES DEL PRINCIPIO DE EQUIVALENCIA: SUSTITUCIÓN DE CAPITALES
La sustitución de unos capitales por otro u otros de vencimientos y/o cuantías diferentes a las anteriores sólo se podrá llevar a cabo si financieramente resultan ambas alternativas equivalentes.
Para ver si dos alternativas son financieramente equivalentes se tendrán que valorar en un mismo momento de tiempo y obligar a que tengan el mismo valor, pudiéndose plantear los siguientes casos posibles:
5.1.1. Determinación del capital común
Es la cuantía C de un capital único que vence en t, conocido, y que sustituye a varios capitales C1, C2, … , Cn, con vencimientos en t1, t2, … ,tn, respectivamente, todos ellos conocidos.
5.1.2. Determinación del vencimiento común
Es el momento de tiempo t en que vence un capital único C, conocido, que sustituye a varios capitales C1, C2, … , Cn, con vencimientos en t1, t2, … ,tn, respectivamente, todos ellos conocidos.
Se tiene que cumplir:
5.1.3. Determinación del vencimiento medio
Es el momento de tiempo t en que vence un capital único C, conocido, que sustituye a varios capitales C1, C2, … , Cn, con vencimientos en t1, t2, … ,tn, respectivamente, todos ellos conocidos.
Se tiene que cumplir:
C = C1 + C2 + … + Cn
EJEMPLO 10
Un señor tiene tres deudas de 2.000, 4.000 y 5.000 euros con vencimientos a los 6, 8 y 10 años, respectivamente, llegando al acuerdo con el acreedor de sustituir las tres deudas por una sola a pagar a los 9 años.
Se pide:
Calcular el importe a pagar en ese momento si la operación se concierta al 8% de interés compuesto anual.
1.er caso: fecha de estudio en 0:
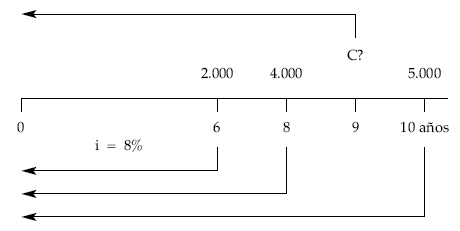
2.000 4.000 5.000 C
———– + ———- + ———– = ———
1,086 1,088 1,0810 1,089
resultando:
C = 11.469,05 €
2.º caso: fecha de estudio en 9:
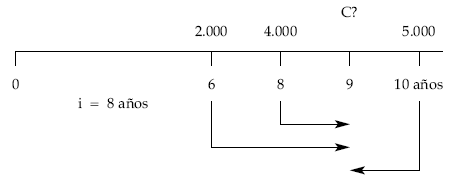
5.000
2.000 x 1,083 + 4.000 x 1,08 + ———- = C
1,08
resultando:
C = 11.469,05 €
EJEMPLO 11
Un señor tiene dos cobros pendientes de 5.000 y 8.000 euros con vencimientos a 3 y 5 años, respectivamente. Si quisiera sustituir ambos capitales por uno sólo, acordándose la operación a un tipo de interés del 6%, calcular el momento del cobro único en los siguientes supuestos:
1.º La cuantía a recibir fuera de 12.000 euros.
2.º La cuantía a recibir fuera de 13.000 euros.
1.er caso: vencimiento común
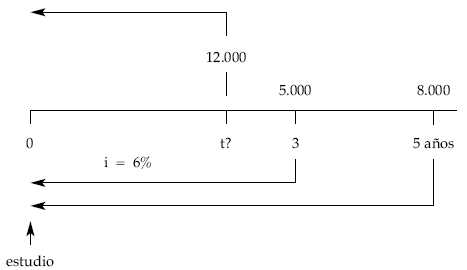
5.000 8.000 12.000
———– + ———– = ———–
1,063 1,065 1,06t
12.000
4.198,10 + 5.978,07 = ———-
1,06t
12.000
10.176,17 = ———–
1,06t
12.000
1,06t = —————-
10.176,17
12.000
log —————-
10.176,17 0,071597
t = ————————– = —————- = 2,83 años
log 1,06 0,025306
2.º caso: vencimiento medio
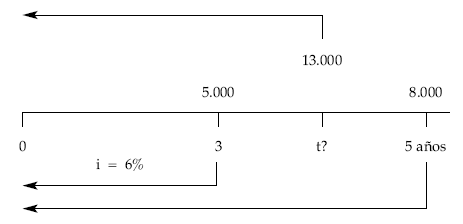
5.000 8.000 13.000
———- + ——— = ————
1,063 1,065 1,06t
13.000
10.176,17 = ———–
1,06t
13.000
log —————-
10.176,17 0,106359
t = ————————– = —————- = 4,20 años
log 1,06 0,025306
Nota. En compuesta no se puede aplicar la fórmula vista en régimen de simple para el cálculo del vencimiento medio:
C1 x t1 + C2 x t2 + … + Cn x tn
t = vencimiento medio = ——————————————–
C1 + C2 + … + Cn




