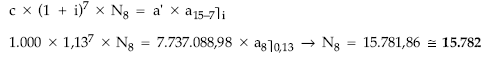En este caso el interés que generan los títulos se va devengando día a día pero no se paga periódicamente a los títulos en circulación, sino que se va acumulando en régimen de compuesta y se les pagará de una vez sólo a aquellos títulos que resulten amortizados en cada sorteo (clase II). Además, la cantidad que el emisor destina periódicamente al pago del empréstito (término amortizativo) y el tipo de interés permanecen constantes (tipo I), y no presenta ninguna otra característica especial (puro).
La estructura de la anualidad será la siguiente:
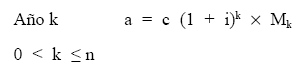
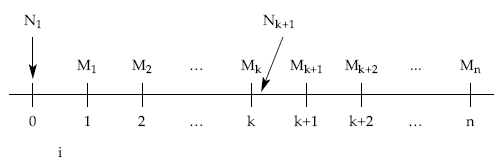
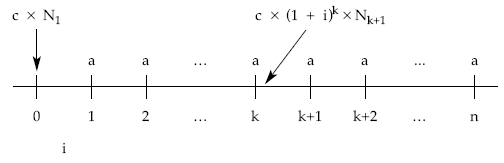
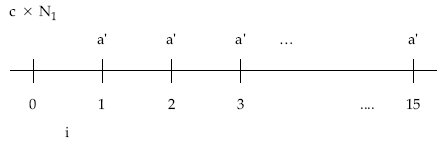
Gráficamente, el esquema de cobros y pagos que el empréstito origina para el emisor un empréstito de N1 títulos, de nominal c, que generan un interés i, a amortizar en n períodos con términos amortizativos constantes, es el siguiente:
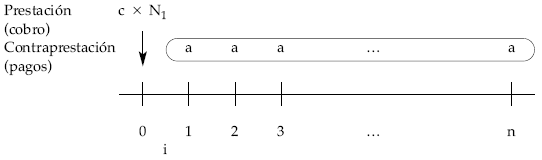
Donde c x N1 representa el importe nominal del empréstito; n, el número de pagos (términos amortizativos) en los que se amortiza; i, el tipo de interés y a, el término amortizativo (anualidad).
6.1. PASOS A SEGUIR
Se trata de seguir un orden con el fin de construir el cuadro de amortización del empréstito, esto es, saber la cantidad a pagar en cada momento (término amortizativo) y a cuántos títulos.
6.1.1. Cálculo del término amortizativo (a)
A pesar de que la estructura del término amortizativo es diferente a la que presenta cuando el cupón se paga periódicamente, el cálculo del importe se realiza igual que en empréstitos clase I. Para calcular dicho término amortizativo bastaría con plantear una equivalencia financiera en el origen entre el nominal del empréstito y la renta formada por los términos que amortizan el empréstito:
![]()
de donde se despeja el término:
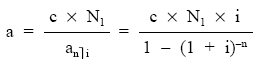
6.1.2. Cálculo de títulos amortizados: ley de recurrencia (Mk)
El número de títulos amortizados en cada sorteo va disminuyendo progresivamente como consecuencia de mantenerse siempre constante el término amortizativo e ir aumentando la cuantía del cupón acumulado a la que tiene derecho cada uno de los títulos amortizados.
Para saber cuál es el número de títulos que en cada sorteo resultan amortizados podemos proceder de dos formas alternativas:
6.1.2.1.
1.ª posibilidad: dando valores a k en la estructura del término amortizativo
Conocida la cuantía del término a pagar en cada período y la cantidad que debe percibir cada título (cupón acumulado y valor de reembolso), se puede saber cuántos títulos se amortizarán en cada momento. Así:
| Período 1: | a = c x (1 + i)1 x M1 | a –> M1 = ————— c x (1 + i) |
| Período 2: | a = c x (1 + i)2 x M2 | a –> M2 = —————– c x (1 + i)2 |
| … |
De esta forma completaríamos el cálculo de títulos amortizados para cualquier sorteo.
6.1.2.2.
2.ª posibilidad: a través de la ley de recurrencia que siguen los títulos amortizados
Se trata de establecer la relación en la que se encuentran los títulos que se van amortizando en cada sorteo. La ley de recurrencia saldrá de la relación, por cocientes, de los términos amortizativos de dos períodos consecutivos cualesquiera, así:
|
Período k: Período k+1: |
a = c x (1 + i)k x Mk a = c x (1 + i)k+1 x Mk+1 |
|
| ———————————– | ||
| a c x (1 + i)k x Mk —- = ———————- a c x (1 + i)k+1 x Mk+1 |
de donde simplificando se obtiene la siguiente expresión:
1
Mk+1 = Mk x ——–
1 + i
En definitiva, los títulos amortizados varían siguiendo una progresión geométrica de razón 1/1 + i, por tanto, cualquier Mk se puede calcular a partir del anterior, del primero o de cualquiera conocido. Con carácter genérico, si se ponen en función del primero:
1
Mk+1 = M1 x ———-
(1 + i)k
6.1.3. Cálculo de títulos amortizados en el primer sorteo (M1)
Una vez calculada M1, todos los demás se podrán obtener aplicando la ley de recurrencia anterior. El cálculo del número de títulos amortizados en el primer sorteo se puede realizar de dos formas posibles:
6.1.3.1. 1.ª posibilidad: a través de la estructura del primer término amortizativo
Período 1: a = c x (1 + i)1 x M1 donde es conocido todo salvo M1
a
M1 = ————-
c x (1 + i)
6.1.3.2. 2.ª posibilidad: a través de los títulos emitidos
En todo empréstito se cumple que la suma aritmética de los títulos amortizados en cada período coincide con el número de títulos puestos en circulación al inicio:
M1 + M2 + M3 + … + Mn = N1
Además, si hacemos uso de la ley de recurrencia entre títulos amortizados, pondremos todos los Mk en función del primero de ellos (M1):
1 1 1
M1 + M1 x ——– + M1 x ———– + … + M1 x ————- = N1
1 + i (1 + i)2 (1 + i)n-1
Simplificando la expresión:
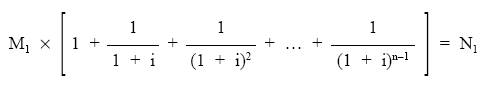
donde el corchete es el valor actual de una renta unitaria, prepagable e inmediata de n términos (el número de sorteos) al tipo de interés que generan los títulos, por tanto:
![]()
de donde:
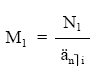
6.1.4. Cálculo del total de títulos amortizados (mk)
Los títulos amortizados transcurrido un período de tiempo cualquiera desde la emisión se pueden obtener de dos formas posibles:
• Por diferencias, entre el número de títulos emitidos y los que aún están en circulación:
mk = N1 – Nk+1
• Por suma de los títulos amortizados hasta la fecha:
mk = M1 + M2 + … + Mk
Además, todos los títulos amortizados, siguiendo la ley de recurrencia que siguen, se pueden poner en función del primero de ellos:
1 1 1
mk = M1 + M1 x ——— + M1 x ———— + … + M1 x ————–
1 + i (1 + i)2 (1 + i)k-1
Simplificando la expresión:
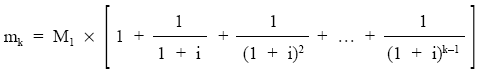
donde el corchete es el valor final de una renta unitaria, pospagable e inmediata, de k términos al tipo i, así pues:
![]()
6.1.5. Cálculo de títulos vivos a principio de cada período (Nk+1)
Podemos plantear este cálculo de varias formas:
6.1.5.1. 1.ª posibilidad: a través de los títulos amortizados
- Método retrospectivo: considerando títulos ya amortizados.
![]()
- Método prospectivo: considerando los títulos pendientes de amortizar.
![]()
6.1.5.2. 2.ª posibilidad: a través de términos amortizativos
Al trabajar con los términos amortizativos se deberán hacer de forma financiera (no bastará con sumar y restar aritméticamente, como en el caso anterior) puesto que los términos incorporan intereses y principal; habrá que mover financieramente las cantidades correspondientes.
• Método retrospectivo, a través de los términos amortizativos pasados.
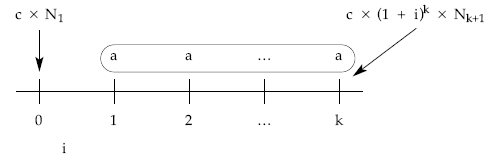
en k se debe cumplir:
lo que se supondría la amortización anticipada en k = [lo recibido – lo pagado]k
en k:
![]()
de donde se despejaría el número de títulos en circulación en ese momento: Nk+1.
• Método prospectivo, a través de los términos amortizativos futuros.
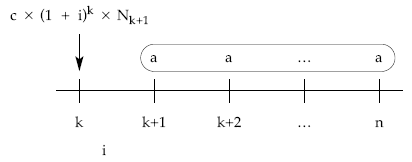
en k se debe cumplir:
lo que se supondría la amortización anticipada en k = [cantidades pendientes de pagar]k
![]()
de donde se despejaría el número de títulos en circulación en ese momento: Nk+1.
6.1.6. Cálculo del importe a pagar de cupones en un período
Los intereses de cualquier período se calcularán a partir del importe total del término amortizativo, una vez deducida la cuantía destinada a la amortización de los títulos.
EJEMPLO 16
Se emite el siguiente empréstito:
- Títulos emitidos: 10.000.
- Nominal del título: 1.000 euros.
- No abono de cupones anuales, acumulándose hasta el momento del sorteo al 12%.
- Sorteos anuales, amortizándose los títulos por el nominal.
- Duración: 3 años.
- Anualidades constantes.
Se pide:
- Anualidad del empréstito.
- Cuadro de amortización.
Solución:
La anualidad constante pagada por el emisor se destina a pagar el nominal junto con el cupón acumulado (en régimen de compuesta) a los títulos que resulten amortizados en cada sorteo. Se trata, pues, de un empréstito puro.
La estructura de la anualidad es:
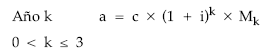
Gráficamente:
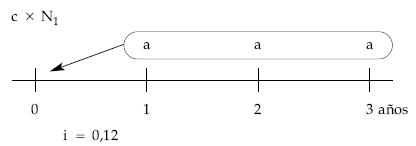
Planteando en el origen la equivalencia entre el nominal del empréstito y las anualidades pagadas:
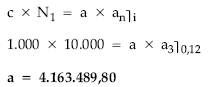
Cuadro de amortización
|
k
|
(1)
|
(2)
|
(3)
|
(4) = (2) x 1.000 x
|
(5) = (4)
x 1,12k |
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Amortización
|
Término
amortizativo |
|
1
2 3 |
10.000
6.283 2.964 |
3.717
3.319 2.964 |
3.717
7.036 10.000 |
4.163.040,0
4.163.353,6 4.164.206,6 |
4.163.040,0
4.163.353,6 4.164.206,6 |
Cálculo de títulos amortizados
|
Año 1 |
a = c x (1 + i)1 x M1
|
||
|
4.163.489,80 = 1.000 x 1,12 x M1
|
M1 = 3.717,40
|
M1 = 3.717
|
|
|
Año 2 |
a = c x (1 + i)2 x M2
|
||
|
4.163.489,80 = 1.000 x 1,122 x M2
|
M2 = 3.319,11
|
M2 = 3.319
|
|
|
Año 3 |
a = c x (1 + i)3 x M3
|
||
|
4.163.489,80 = 1.000 x 1,123 x M3
|
2.963,49
M3 = ————– 9.999 |
2.964
M3 = ———– 10.000 |
Al destinarse la anualidad exclusivamente al pago del cupón acumulado y la amortización por el nominal a los títulos amortizados, el valor de reembolso (amortización) coincide con el importe del término amortizativo del empréstito.
6.2.
EMPRÉSTITO DE CUPÓN ACUMULADO CONSTANTE Y ANUALIDAD CONSTANTE CON CARACTERÍSTICAS COMERCIALES
Todas las expresiones empleadas hasta ahora son válidas para empréstitos denominados puros, es decir, aquellos en los que el término amortizativo se destina exclusivamente al pago del cupón acumulado (constante) y a amortizar por el nominal a los títulos que corresponda.
No obstante, podemos encontrarnos con empréstitos en los que el emisor haya previsto alguna característica comercial. En estos casos, habrá que «preparar el empréstito» para poder aplicar las expresiones anteriores.
Los pasos a seguir para trabajar con empréstitos de cupón acumulado cuando tienen características comerciales son:
1.º Determinar la composición de la estructura de la anualidad siguiendo el siguiente orden:
Anualidad = Intereses acumulados + Amortización + Lotes + Gastos de administración
2.º Proceso de normalización: el objetivo final es dejar la estructura de partida en una equivalente en la que la anualidad se destine exclusivamente a pagar el cupón acumulado y a amortizar por el nominal los títulos.
El resultado de la normalización será una estructura pura:
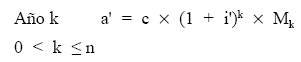
donde:
a’: es la anualidad normalizada
i’: es el tanto normalizado
3.º Las expresiones, fórmulas y reglas de cálculo de anualidad, títulos vivos, amortizados y total de amortizados, comentadas para el empréstito puro ahora son válidas pero cambiando a por a’ e i por i’.
EJEMPLO 17
Se emite el siguiente empréstito:
- Títulos emitidos: 50.000.
- Nominal del título: 1.000 euros.
- No abono de cupones anuales, acumulándose hasta el momento del sorteo al 13%.
- Sorteos anuales, repartiéndose un premio de 1.000 euros para cada uno de los 100 primeros títulos sorteados cada año.
- Gastos de administración del 1‰ sobre las cantidades pagadas anualmente a los obligacionistas.
- Duración: 15 años.
- Anualidad constante.
Se pide:
- Anualidad del empréstito.
- Número de títulos en circulación a principios del octavo año.
Solución:
Cálculo de la anualidad
Es un empréstito de cupón acumulado (clase II) siendo el tipo de interés constante. Además, la anualidad constante incorpora la devolución de los títulos por el nominal junto con el cupón acumulado, un lote constante de 100.000 euros (1.000 x 100) y unos gastos de administración calculados sobre las cantidades cobradas por los obligacionistas. La estructura de la anualidad es:
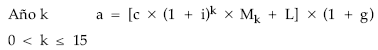
Los pasos de la normalización son:
1.º Dividir por 1 + g la igualdad:
a
———- = c x (1 + i)k x Mk + L
1 + g
2.º Pasar el lote al primer miembro de la igualdad:
a
———- – L = c x (1 + i)k x Mk
1 + g
La estructura conseguida tiene forma pura, pues se destina a amortizar los títulos pagándoles el nominal y el cupón acumulado:
Siendo:
a
a’ = ———- – L
1 + g
queda la anualidad normalizada:
a’ = c x (1 + i)k x Mk
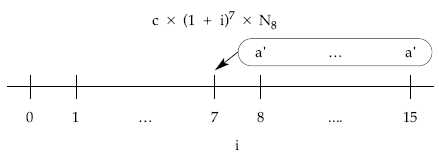
Gráficamente:
Planteando la equivalencia en el origen entre el nominal del empréstito y la renta formada por las anualidades normalizadas al tanto del cupón (porque la normalización no le ha afectado):
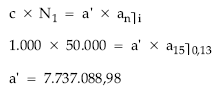
Finalmente, de la estructura de la anualidad normalizada obtenemos la anualidad definitiva del empréstito:
a
a’ = ——— – L
1 + g
a
7.737.088,98 = ————— – 100.000
1 + 0,001
a = 7.844.926,07
Títulos en circulación a principios del 8.º año
Por el método prospectivo, se ha de cumplir la siguiente igualdad en el momento 7: