Este sistema de amortización se caracteriza porque:
- Los términos amortizativos permanecen constantes, y
- El tanto de valoración permanece constante.
ambos durante toda la vida del préstamo.
De esta forma al principio la mayor parte de la cuota son intereses, siendo la cantidad destinada a amortización muy pequeña. Esta proporción va cambiando a medida que el tiempo va transcurriendo.
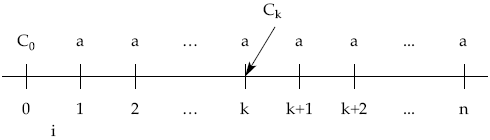
Gráficamente, el esquema de cobros y pagos que origina para el prestatario el préstamo es el siguiente:
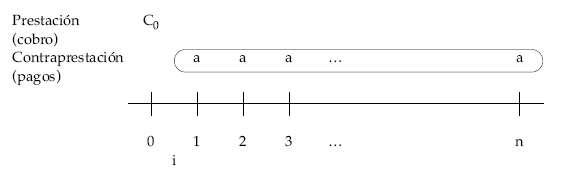
Donde C0 representa el importe del préstamo, n el número de pagos en los que se amortiza el préstamo, a el término amortizativo e i el tipo de interés de la operación.
4.1. PASOS A SEGUIR
Se trata de ver los cálculos a realizar con el fin de construir el cuadro de amortización del préstamo, esto es, saber la cantidad a pagar en cada momento (término amortizativo) y su descomposición en cuota de amortización (Ak) y cuota de interés (Ik), así como otros datos como capitales vivos en cada momento (Ck) sobre los que calcular los intereses y el total amortizado (mk).
4.1.1. Cálculo del término amortizativo (a)
Los pagos constantes que se realizan durante la vida del préstamo incorporan, en parte el coste del aplazamiento (cuota de interés), en parte la devolución de una porción de la deuda (cuota de amortización). Para eliminar los intereses bastaría con actualizar los términos amortizativos a la tasa de interés del préstamo, con lo cual sólo quedarían las cuotas de principal, que sumadas coinciden con el importe del préstamo.
Es decir, planteamos una equivalencia financiera en el origen entre el importe del préstamo y la renta formada por los términos amortizativos:
![]()
de donde se despeja el término:
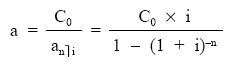
4.1.2. Cálculo de las cuotas de amortización: ley de recurrencia
4.1.2.1. 1.ª posibilidad: a través de la estructura del término amortizativo
Una vez calculado el término amortizativo, se cumple lo siguiente:
Período 1: a = I1 + A1 = C0 x i + A1, de donde se despeja A1 (ya que lo demás se conoce).
Período 2: a = I2 + A2 = C1 x i + A2 = (C0 – A1) x i + A2, y despejamos A2.
Período 3: a = I3 + A3 = C2 x i + A3 = (C1 – A2) x i + A3, y despejamos A3.
y así se continuaría hasta calcular el resto de cuotas de amortización.
4.1.2.2. 2.ª posibilidad: a través de la ley de recurrencia que siguen las cuotas de amortización
Al ser constante el término amortizativo las cuotas de amortización necesariamente tendrán que ir creciendo, mientras que las cuotas de intereses decrecerán (porque se van calculando sobre capitales vivos cada vez menores). Y además, lo hacen siguiendo una ley matemática (ley de recurrencia).
La ley de recurrencia es la relación en la que se encuentran dos términos consecutivos, en este caso, las cuotas de amortización y para buscarla se relacionan por diferencias los términos amortizativos de dos períodos consecutivos cualesquiera, así:
Período k: a = Ik + Ak = Ck-1 x i + Ak
Período k+1: a = Ik+1 + Ak+1 = Ck x i + Ak+1
——————————————
a – a = (Ck-1 – Ck) x i + Ak – Ak+1
siendo Ck-1 – Ck = Ak, queda:
0 = Ak x i + Ak – Ak+1
de donde se obtiene:
Ak+1 = Ak x (1 + i)
Al aplicar esta ley para cualesquiera dos períodos consecutivos, se observa que varían siguiendo una progresión geométrica de razón 1 + i , por tanto, cualquier cuota se puede calcular a partir de la anterior, de la primera o de cualquiera conocida. Con carácter genérico, se pondrán en función de la primera –que es la más fácil de obtener–:
Ak+1 = A1 x (1 + i)k
Es por esto, el aumento de las cuotas de amortización con el transcurso del tiempo, por lo que a este sistema se le conoce como método progresivo.
4.1.3. Cálculo de la primera cuota de amortización (A1)
Una vez calculada la primera cuota, todas las demás se podrán obtener aplicando la ley de recurrencia anterior. El cálculo de la primera cuota de amortización se puede realizar de dos formas posibles:
4.1.3.1.
1.ª posibilidad: a través de la estructura del primer término amortizativo
Período 1: a = I1 + A1 = C0 x i + A1 —> A1 = a – C0 x i
4.1.3.2. 2.ª posibilidad: por la definición de capital prestado
En todo préstamo se cumple que la suma aritmética de todas las cuotas de amortización es el importe del préstamo:
A1 + A2 + A3 + … + An = C0
Además en este sistema amortizativo todas las cuotas de amortización se pueden poner en función de la primera de ellas, como se ha visto anteriormente:
A1 + A1 (1 + i) + A1 (1 + i)2 + … + A1 (1 + i)n-1 = C0
Simplificando la expresión, sacando factor común en el primer miembro A1:
A1 x [1 + (1 + i) + (1 + i)2 + … + (1 + i)n-1] = C0
donde el corchete es el valor final de una renta unitaria, pospagable e inmediata de n términos (el número de cuotas de amortización) al tanto del préstamo, por tanto:
![]()
de donde:
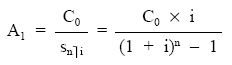
4.1.4. Cálculo del total amortizado después de k períodos (mk)
Conocer la totalidad de la deuda amortizada en un momento de tiempo concreto se puede hacer de dos formas posibles:
• Por diferencia, entre el importe del préstamo y lo que aún se debe:
mk = C0 – Ck
• Por sumas de cuotas de amortización practicadas hasta la fecha:
mk = A1 + A2 + … + Ak
Además todas las cuotas de amortización se pueden poner en función de la primera de ellas:
mk = A1 + A1 (1 + i) + A1 (1 + i)2 + … + A1 (1 + i)k-1
Simplificando la expresión:
mk = A1 x [1 + (1 + i) + (1 + i)2 + … + (1 + i)k-1]
donde el corchete es el valor final de una renta unitaria, pospagable e inmediata, de k términos al tanto del préstamo, por tanto:
![]()
4.1.5. Cálculo del capital vivo a principio del período k+1 (Ck)
4.1.5.1. 1.ª posibilidad: a través de las cuotas de amortización
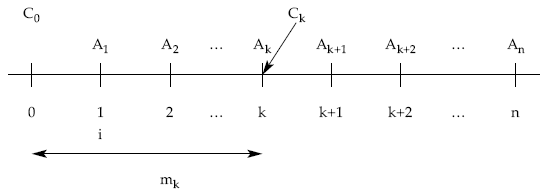
Bien considerando las cuotas de amortización ya satisfechas (método retrospectivo):
![]()
Bien considerando las cuotas de amortización pendientes (método prospectivo):
![]()
4.1.5.2. 2.ª posibilidad: a través de términos amortizativos
Al trabajar con los términos amortizativos se deberán hacer en términos financieros (no bastará con sumar y restar aritméticamente, como en el caso anterior) puesto que los términos incorporan intereses y principal; habrá que mover financieramente las cantidades correspondientes.
4.1.5.3.
1.ª posibilidad: método retrospectivo, a través de los términos amortizativos pasados
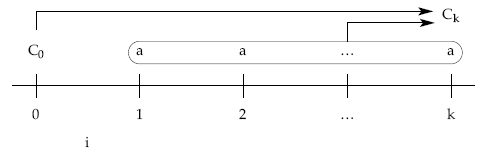
En k se debe cumplir:
lo que se debe en k = [lo recibido – lo pagado]k
Por tanto en k:
![]()
4.1.5.4.
2.ª posibilidad: método prospectivo, a través de los términos amortizativos futuros
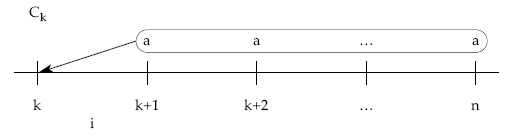
En k se debe cumplir:
lo que supondría la cancelación total en k = [cantidades pendientes de pagar]k
Por tanto en k:
![]()
4.1.6. Cálculo de la cuota de interés del período k+1 (Ik+1)
Los intereses de cualquier período se calcularán a partir de la deuda pendiente a principios de ese período, al tanto efectivo vigente durante el mismo.
Ik+1 = Ck x i
EJEMPLO 4
Construir el cuadro de amortización del siguiente préstamo:
- Importe: 100.000 euros.
- Duración: 3 años.
- Tipo de interés: 10% anual.
- Términos amortizativos anuales constantes.
|
|
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
|
Años
|
Término amortizativo
|
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Capital vivo
|
|
0
1 2 3 |
40.211,48
40.211,48 40.211,48 |
10.000,00
6.978,85 3.655,59 |
30.211,48
33.232,63 36.555,89 |
30.211,48
63.444,11 100.000,00 |
100.000,00
69.788,52 36.555,89 |
|
Total
|
120.634,44
|
20.634,44
|
100.000,00
|
|
|
Descripción de los pasos a seguir para construir el cuadro:
(1) Se calcula el importe del pago total a realizar (término amortizativo) a través de la fórmula anterior.
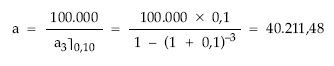
(2) La cuota de interés se calcula sobre el capital pendiente a principios del período correspondiente (5) y se pagan al final del período anterior.
(3) La cantidad destinada a amortizar será la diferencia entre el total pagado en el período (1) y lo que se dedica a intereses (2).
(4) Se calcula el total amortizado por sumas parciales de las cuotas de amortización practicadas hasta la fecha.
(5) La deuda pendiente se obtendrá de restar al capital vivo a principios de cada período la cuota de amortización de ese mismo período, o bien, al importe del préstamo se le resta el total amortizado (4) ya acumulado.




