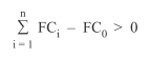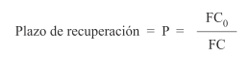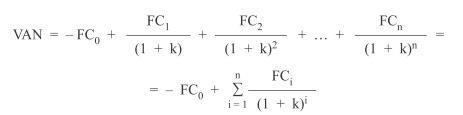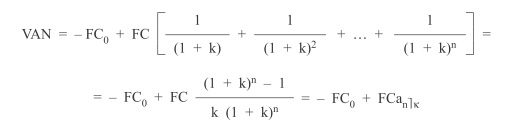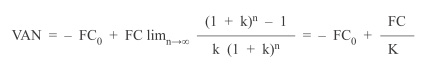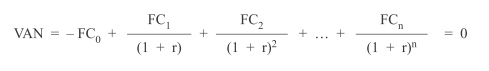La realidad de un proyecto de inversión puede analizarse a modo de proceso temporal compuesto por dinámicas de cobro y pago temporalizadas, concepto comúnmente conocido como «flujo de caja neto» o cash flow.
De forma sintética cualquier proyecto de inversión se puede representar de la siguiente forma:
El consecuente análisis temporal y su evaluación convergen alrededor de los siguientes conceptos y cálculos:
- Costes de inversión. Se agrupan en dos apartados, el coste del bien, o activo sujeto de la inversión, y los costes operativos, o derivados de la explotación de la misma.
- Duración de la inversión. Periodo de vida o tiempo en que estará funcionando normalmente la inversión o que esta generará los flujos de fondos (FC) correspondientes.
- Cálculo de las entradas de fondos. Son los cobros o flujos de entrada (FE) de los ingresos o de las ventas producidas por el proyecto de inversión.
- Cálculo de las salidas de fondos. Son los pagos o flujos de salida (FS) de los distintos conceptos de coste:
– Desembolso inicial.
– Costes operativos o de la explotación.
– Impuestos derivados de los beneficios obtenidos por la inversión.
- Cálculo de los flujos de fondos. Los flujos netos de caja se obtendrán por diferencia entre los flujos de entradas y los de salidas de fondos, dando lugar a los saldos con sus correspondientes signos positivos o negativos, es decir:
± FCi = FEi – FSi
(i = 1, 2,…, n periodos de tiempo)
- Condiciones de realización de la inversión. Existen dos condiciones, a saber:
– Condición de posibilidad o economicidad de la inversión:
Siendo FC0 el desembolso o pago inicial del proyecto.
– Condición de efectuabilidad o de rentabilidad de la inversión:
r > k
Siendo r la tasa de rendimiento de la inversión y k el coste del capital o de los recursos financieros invertidos.
Con el fin de facilitar un mejor entendimiento de todos estos conceptos y formas de cálculo, se expone el siguiente ejemplo:
EJEMPLO 1
La empresa «Quinito» está considerando la adquisición de un determinado recurso para mejorar su capacidad de producción, en virtud de los datos del departamento financiero y el suministrador se configura el siguiente escenario:
|
Conceptos
|
Duración (años)
|
||||
|
0
|
1
|
2
|
3
|
4
|
|
| 1. Ingresos de proyecto |
–
|
33
|
47
|
55
|
38
|
| 2. Costes del proyecto |
– 44
|
– 22
|
– 24
|
– 28
|
– 25
|
| 3. Amortización de la inversión |
–
|
– 11
|
– 11
|
– 11
|
– 11
|
| 4. Beneficio del periodo |
–
|
0
|
12
|
16
|
2
|
| 5. Impuestos sobre beneficio |
–
|
–
|
4,2
|
5,6
|
0,7
|
| 6. Beneficio neto |
–
|
0
|
7,8
|
10,4
|
1,3
|
| 7. Flujos netos de caja {(1) – (2) – (5)} |
– 44
|
0
|
18,8
|
21,4
|
12,3
|
De esta información se interpreta que en la tarea de evaluación de proyectos se deben utilizar los flujos de caja en vez de los beneficios de cada año, aunque por diferentes causas se suelen usar los beneficios netos. En este ejemplo se constata que se cumple la primera condición, es decir, que el desembolso inicial (44) es inferior a la suma de los flujos de caja (52,5), quedando pendiente el cálculo de la tasa interna de rendimiento del proyecto (r), derivada de su temporalidad, supere o no el coste de los recursos financieros aplicados (k) en tales periodos.
En este sentido, existen diferentes criterios para efectuar la tarea de inversión: el criterio del plazo de recuperación o pay back, el criterio del valor actual neto y el criterio de la tasa interna de rendimiento.
4.1. CRITERIO DE PLAZO DE RECUPERACIÓN O PAY BACK
Este criterio se articula alrededor del plazo de recuperación de la inversión, es decir, la identificación del tiempo que se tarda en recuperar el desembolso inicial. En el caso de flujos de caja no constantes (situación normal) se deben ir acumulando en el tiempo hasta que se iguale el desembolso inicial. Para el caso de los flujos constantes:
FC1 = FC2 = … = FCn = FC
Basándose en este criterio la inversión más conveniente resultará de analizar el pay back más corto, lo que supone el criterio preferido en épocas de crisis política o económica. No obstante, este método recibe las siguientes críticas:
- No tiene en cuenta la temporalidad de los flujos de fondos, es decir, no los actualiza a partir de sus diferentes vencimientos.
- No considera el efecto de los flujos de fondos a partir del plazo de recuperación.
- Es un criterio que se basa en la liquidez y no en la rentabilidad, al solo tener en cuenta el tiempo más corto de recuperación y no la condición de efectuabilidad (r > k).
En el marco del ejemplo, el pay back se lograría entre el tercer y el cuarto año, concretamente al final del tercero se recuperarán 40,2 millones y los 3,8 restantes se lograrían al finalizar el primer cuatrimestre (siendo regulares los flujos de caja).
4.2. CRITERIO DEL VALOR ACTUAL NETO
El conocido valor actual neto (VAN) es el valor actualizado de todos los flujos de caja esperados, tanto positivos como negativos, siendo kn los tipos de descuento o interés, de tales fondos y periodos.
En el caso de que el tipo de descuento sea constante o independiente del tiempo k1 = k2 = … = kn = k, el valor capital en el momento actual será:
Si los flujos de caja son iguales o constantes: FC1 = FC2 =…= FCn = FC, la anterior fórmula se transformará en esta:
Siendo a![]() el valor actual de una anualidad (renta) unitaria al tipo de interés k y durante n periodos.
el valor actual de una anualidad (renta) unitaria al tipo de interés k y durante n periodos.
Si además de ser constantes los flujos de caja, la duración del proyecto es ilimitada, la fórmula anterior queda convertida en esta:
Siendo 1/k el concepto de una renta o anualidad unitaria constante.
Los cálculos del VAN resultan más sencillos si se tiene en cuenta la disponibilidad de tablas financieras en la que se pueden obtener ciertos valores.
Siguiendo este criterio, la decisión de inversión se basa en el razonamiento siguiente:
- Si VAN > 0, la inversión debe llevarse a cabo ya que se aumenta el patrimonio de la empresa.
- Si VAN < 0, la inversión no debe realizarse ya que disminuirá el patrimonio de la empresa.
- Si VAN = 0, es igual que la inversión se realice o no, ya que no se modifica el patrimonio empresarial.
4.3. CRITERIO DE LA TASA INTERNA DE RENDIMIENTO
La tasa interna de rendimiento (TIR) o tasa de retorno (r) son los tipos que hacen que el VAN sea igual a cero.
Este criterio proporciona un indicador de rentabilidad actualizando los valores y relativizándolos, de esta forma la decisión se plantea así:
- Si r > k, la inversión puede realizarse.
- Si r < k, no interesa llevar a cabo la inversión.
- Si r = k, la situación es de indiferencia, por lo que con decisores con aversión al riesgo tampoco se realizaría.
La puesta en práctica de este criterio ostenta ciertos problemas de cálculo, sobre todo si la inversión cuenta con más de un flujo de caja negativo (inversión no simple), lo que implica una ecuación de grado n con n raíces o soluciones. En todo caso, si no se dispone de programas de cálculo, se recomienda la técnica de prueba y error con la ayuda de las mencionadas tablas financieras hasta llegar al valor que verifica la ecuación.
EJEMPLO 2
Siguiendo con el ejemplo mostrado:
|
18,8
|
21,4
|
12,3
|
||||||||||
|
VAN
|
=
|
– 44
|
+
|
0
|
+
|
_____
|
+
|
_____
|
+
|
_____
|
=
|
0
|
|
(1 + r)2
|
(1 + r)3
|
(1 + r)4
|
Donde r = 6,38%, si el coste del capital es del 10 por 100 resulta claro que no desearía efectuarse la inversión.
Al margen de la posible existencia de tasas múltiples también puede surgir otra incidencia en el valor del proyecto de inversión, a saber, la tasa de reinversión de los fondos intermedios, suponiendo la utilización del mismo tipo o coste r.
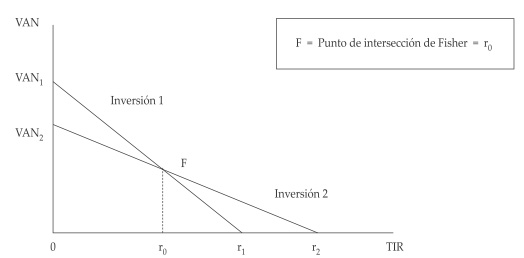
En la representación gráfica de proyectos con VAN y TIR diferentes, puede ocasionarse un punto de cruce, intersección o indiferencia de ambos, punto conocido como el «punto de Fisher».
|
Figura 6. Relación entre VAN y la TIR
|