La valoración de títulos procedentes de un empréstito cualquiera implica conocer las cuantías de los derechos económicos futuros que dicho título conlleva y actualizarlos al momento de estudio a un tipo adecuado (tanto de mercado).
Definiciones:
- Valor de un título en el momento k (principios del período k+1), Vk, es el resultado de actualizar al tanto de mercado (im) todos los derechos económicos futuros que el título conlleva.
- Usufructo de un título en el momento k (principios del período k+1), Uk, es el resultado de actualizar al tanto de mercado (im) todos los cupones futuros que el título conlleva.
- Nuda propiedad de un título en el momento k (principios del período k+1), Nk , es el resultado de actualizar al tanto de mercado (im) el valor de reembolso del título.
De las definiciones anteriores se deduce la necesidad de conocer para estos cálculos:
- Cuantía de los derechos económicos futuros del título (cupones, valor de reembolso y lotes).
- Número de capitales (derechos económicos) a considerar.
El número de derechos está en función del tiempo que el título esté en circulación, o sea, del momento en que resulte amortizado. Por ello debemos considerar un horizonte temporal para su estudio, pudiéndose contemplar tres posibilidades:
- Conocer de antemano el momento del sorteo del título.
- Estimar un período de vida para el título, tomándose como tal la vida media (o mediana) del conjunto de títulos del empréstito en la fecha de estudio.
- Considerar un valor medio, es decir, calcular un valor global para el conjunto del empréstito y dividirlo proporcionalmente entre el número de títulos vivos en la fecha de estudio.
Aplicaremos estos escenarios a los diferentes tipos de empréstitos estudiados.
9.3.1. Empréstitos clase I, tipo I, normal
Empréstitos con término amortizativo constante y cupón constante y vencido pagadero a los títulos en circulación en cada momento.
La estructura del término amortizativo es la siguiente:
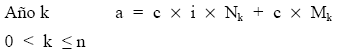
Se trata de realizar el cálculo del valor, usufructo y nuda propiedad de un título procedente de este empréstito en un momento cualquiera considerando los posibles escenarios antes comentados.
Caso 1: el título resultará amortizado en el momento k+t
Estamos suponiendo que se conoce con absoluta certeza el momento en que resultará amortizado el título estudiado.
Gráficamente el esquema de flujos pendientes desde la fecha de estudio (k) hasta el momento del sorteo (k + t):
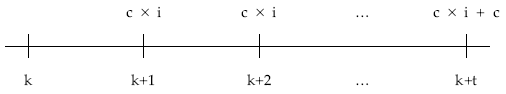
Aplicando las definiciones de usufructo, nuda propiedad y valor:
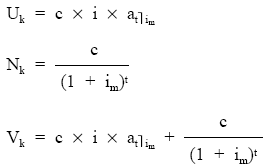
EJEMPLO 25
Se emite el siguiente empréstito:
- Títulos emitidos: 20.000.
- Nominal título: 1.000 euros.
- Cupón anual: 50 euros.
- Duración: 4 años.
- Prima amortización: 200 euros.
- Anualidad constante.
Se pide:
- Valor, usufructo y nuda propiedad en el origen de un título que resultará amortizado en el segundo sorteo, siendo el tanto de mercado el 4%.
- Valor, usufructo y nuda propiedad en el origen de un título que resultará amortizado en el cuarto sorteo, siendo el tanto de mercado el 4%.
Solución:
a) Si el título se amortiza en el segundo año:
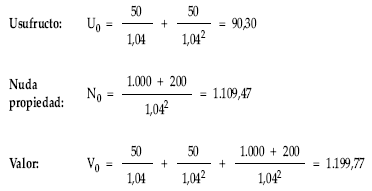
b) Si el título se amortiza en el cuarto año:
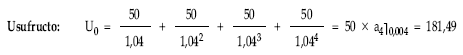
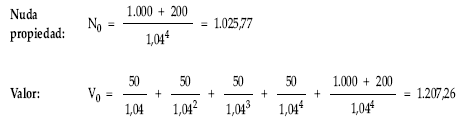
Caso 2: tomando como estimación la vida media del empréstito en la fecha de estudio
Ahora desconocemos el momento en que resultará amortizado el título estudiado, por ello se toma como estimación la vida media calculada para todo el empréstito en la fecha donde estamos valorando.
Gráficamente el esquema de flujos pendientes desde la fecha de estudio (k) hasta el momento del sorteo (k + Vm):
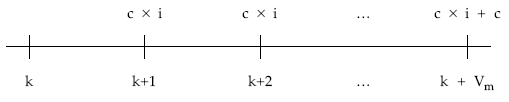
Aplicando de nuevo las definiciones de usufructo, nuda propiedad y valor:
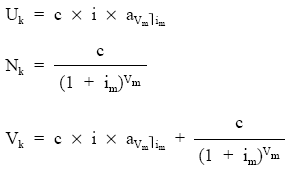
Caso 3: considerando valores medios
En los dos casos anteriores, bien conociendo la fecha del sorteo bien tomando como horizonte de estudio la vida media del empréstito, se considera únicamente el título objeto de valoración. Ahora, por el contrario, se trabaja con el conjunto de títulos vivos en la fecha de estudio del empréstito, para, después, estimar el valor medio de cada uno de ellos.
El esquema de flujos pendientes del empréstito en su conjunto es el siguiente:
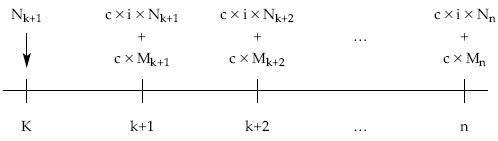
Aplicando las definiciones de usufructo, nuda propiedad y valor, en este caso aplicados para el conjunto del empréstito (valores totales o globales):
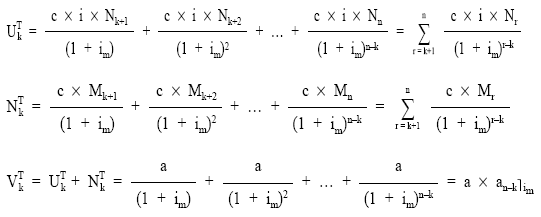
Estos valores globales se repartirán entre el número de títulos vivos en la fecha de estudio (Nk+1), para obtener los valores medios por título de usufructo, nuda propiedad y valor:
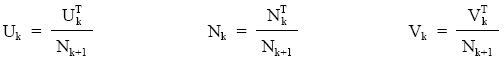
No obstante, este método de cálculo exige conocer las cantidades destinadas al pago de cupones y de amortización en cada momento desde la fecha de estudio hasta el final del empréstito (cuadro de amortización). Un sistema alternativo sería la utilización del siguiente sistema de ecuaciones, que solamente se podrá emplear en el supuesto de que se cumplan los tres siguientes requisitos:
- El cupón periódico se mantiene constante desde la fecha de estudio hasta n.
- El tanto de mercado (im) sea diferente al tanto del cupón (i).
- Encontrarse al principio de un período.
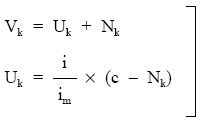
Donde:
i: Tipo del cupón del título.
im: Tipo de mercado.
c: Nominal del título.
Para su resolución se calculará previamente el Vk, según la expresión:
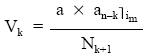
y del sistema se despejarán Uk y Nk.
| Nota: este sistema de ecuaciones también se puede aplicar a cualquier empréstito de cupón periódico con anualidad variable (clase I, tipo II). |
EJEMPLO 26
Se emite el siguiente empréstito:
- Títulos emitidos: 30.000.
- Nominal título: 1.000 euros.
- Cupón anual: 100 euros.
- Duración: 3 años.
- Anualidad constante.
Se pide:
- Cuadro de amortización.
- Valor, usufructo y nuda propiedad en el origen a un tanto de mercado del 12%.
Solución:
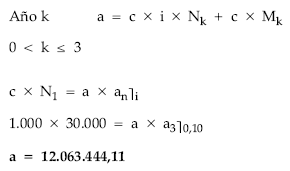
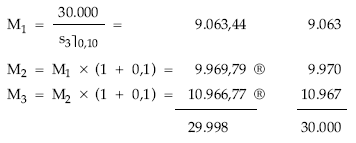
Cuadro de amortización
|
Año
|
Títulos vivos
|
Título amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 |
30.000
20.937 10.967 |
9.063
9.970 10.967 |
9.063
19.033 30.000 |
3.000.000
2.093.700 1.096.700 |
9.063.000
9.970.000 10.967.000 |
12.063.000
12.063.700 12.063.700 |
Valor, usufructo y nuda propiedad en el origen al tanto im = 12%:
1.ª posibilidad: aplicando las definiciones

2.ª posibilidad: aplicando el sistema de ecuaciones
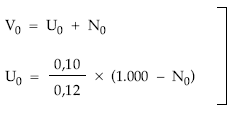
Aplicando la definición de valor medio de un título se obtiene Vo:
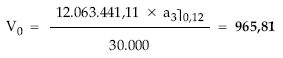
Del sistema se despeja la nuda propiedad y a continuación el usufructo:
![]()
9.3.2. Incidencia de las distintas características comerciales
Cuando existan en el empréstito características comerciales, será preciso distinguir cómo afectan a la hora de valorar el título. Será necesario, pues, un estudio individualizado de cada una de las posibles características que pueden aparecer.
De igual forma, se podrá aplicar indistintamente las definiciones o aplicar el sistema de ecuaciones, si bien considerando cómo afecta la(s) característica(s) que en cada caso se presenten.
Pasamos al estudio de cada característica comercial:
9.3.2.1. Prima de amortización
Afecta a la nuda propiedad y al valor, pero no al usufructo.
El sistema queda como sigue:
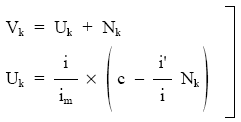
Donde:
i: Tipo del cupón del título.
im: Tipo de mercado.
c: Nominal del título.
i’: Tipo normalizado del empréstito.
EJEMPLO 27
Se emite el siguiente empréstito:
- Títulos emitidos: 1.000.
- Nominal título: 1.000 euros.
- Interés anual: 6%.
- Duración: 4 años.
- Valor de reembolso de los títulos: 1.200 euros.
- Anualidad constante.
Se pide:
Calcular el valor medio de un título transcurrido 1 año desde la emisión, siendo el tanto de mercado el 7% efectivo anual.
Solución:
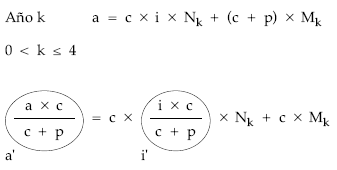
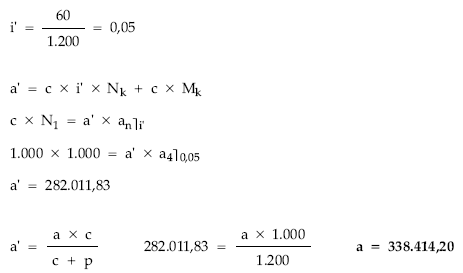
Cálculo de los títulos amortizados
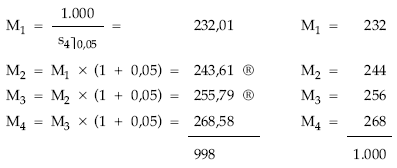
Cuadro de amortización
|
|
(1)
|
(2)
|
(3)
|
(4) = (1) x 60
|
(5) = (2) x 1.200
|
(6) = (4) + (5)
|
|
Año
|
Títulos vivos
|
Título amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 4 |
1.000
768 524 268 |
232
244 256 268 |
232
476 732 1.000 |
60.000
46.080 31.440 16.080 |
278.400
292.800 307.200 321.600 |
338.400
338.880 338.640 337.680 |
Valor, usufructo y nuda propiedad en 1 al tanto im = 7%
1.ª posibilidad: aplicando las definiciones

2.ª posibilidad: aplicando el sistema de ecuaciones
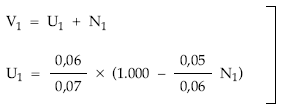
Aplicando la definición de valor medio de un título se obtiene V1:
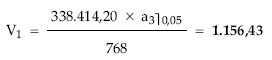
Del sistema se despeja la nuda propiedad y a continuación el usufructo:
![]()
9.3.2.2. Amortización seca
Afecta al usufructo y al valor, pero no a la nuda propiedad.
El sistema de ecuaciones visto anteriormente considera que la amortización seca no es una pérdida de cupón sino una prima de amortización negativa, por lo que infravalora la nuda propiedad y da más valor al usufructo.
Por este motivo, en lugar de aplicar el sistema se calcula el valor y la nuda propiedad aplicando las definiciones técnicas y el usufructo se obtiene por diferencias.
EJEMPLO 28
Se emite el siguiente empréstito:
- Títulos emitidos: 1.000.
- Nominal título: 1.000 euros.
- Interés anual: 5%.
- Duración: 3 años.
- Los títulos amortizados pierden el último cupón.
- Anualidad constante.
Se pide:
Calcular el valor medio de un título transcurrido 1 año desde la emisión, siendo el tanto de mercado el 4% efectivo anual.
Solución:
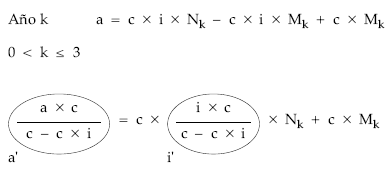
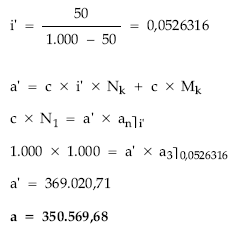
Cálculo de los títulos amortizados
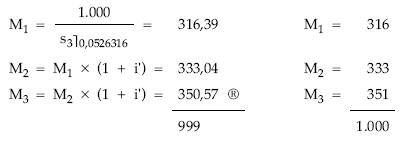
Cuadro de amortización
|
|
(1)
|
(2)
|
(3)
|
(4) = [(1) – (2)] x 50
|
(5) = (2) x 1.200
|
(6) = (4) + (5)
|
|
Año
|
Títulos vivos
|
Título amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 |
1.000
684 351 |
316
333 351 |
316
649 1.000 |
34.200
17.550 |
316.000
333.000 351.000 |
350.200
350.550 351.000 |
Valor, usufructo y nuda propiedad en 1 al tanto im = 4%
1.ª posibilidad: empleando los datos del cuadro
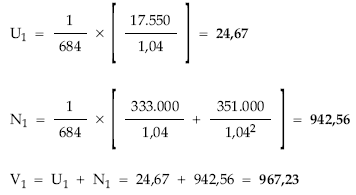
2.ª posibilidad: aplicando las definiciones
Aplicando la definición de valor medio de un título se obtiene V1:
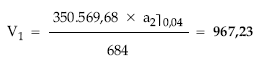
Aplicando la definición de nuda propiedad media se obtiene N1:
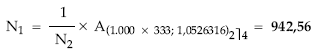
El usufructo se obtiene por diferencia entre valor y nuda propiedad:
![]()
9.3.2.3. Lotes
Afecta al valor, pero no al usufructo ni a la nuda propiedad.
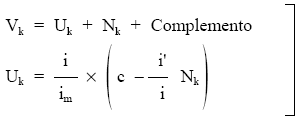
Donde el complemento es la actualización de los lotes futuros por obligación en circulación:
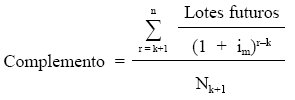
En este caso, previamente deberemos calcular el valor (por el mismo procedimiento) y el complemento aplicando su definición. Del sistema se despejarán usufructo y nuda propiedad.
9.3.2.4. Gastos de administración
No afectan ni al usufructo ni a la nuda propiedad ni al valor.
Hay que tener en cuenta que, de existir, los gastos de administración forman parte de la anualidad del empréstito, por lo que habrá que quitarlos y a continuación se utiliza el sistema de ecuaciones correspondiente.
EJEMPLO 29
Se emite el siguiente empréstito:
- Títulos emitidos: 30.000.
- Nominal título: 1.000 euros.
- Cupón anual: 100 euros.
- Duración: 3 años.
- Reparto de un premio de 200 euros a 1.000 títulos amortizados cada año.
- Gastos de administración del 1‰ de las cantidades pagadas.
- Todos los años se amortizan el mismo número de títulos.
Se pide:
- Cuadro de amortización.
- Valor, usufructo y nuda propiedad en el origen a un tanto de mercado del 12%.
Solución:
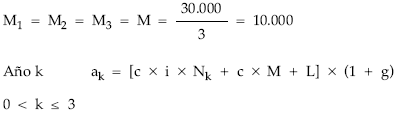
Cuadro de amortización
|
Año
|
Títulos vivos
|
Título amortiz.
|
Intereses
|
Amortiz.
|
Lotes
|
Gastos admón.
|
Término amortizativo
|
|
1
2 3 |
30.000
20.000 10.000 |
10.000
10.000 10.000 |
3.000.000
2.000.000 1.000.000 |
10.000.000
10.000.000 10.000.000 |
200.000
200.000 200.000 |
13.200
12.200 11.200 |
13.213.200
12.212.200 11.211.200 |
Valor, usufructo y nuda propiedad en el origen al tanto im = 12%
1.ª posibilidad: aplicando las definiciones
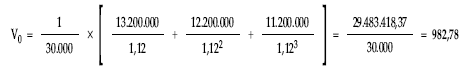
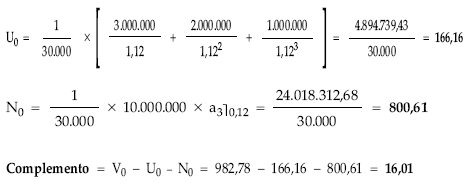
2.ª posibilidad: aplicando el sistema de ecuaciones
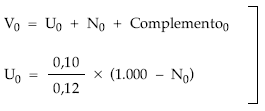
Aplicando las definiciones calculamos nuda propiedad y complemento:
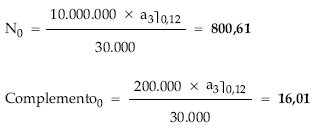
Del sistema se despeja el usufructo y a continuación el valor:
![]()
9.3.2.5. Cupón fraccionado
Afecta al usufructo e, indirectamente, al valor, pero no a la nuda propiedad.
El sistema de ecuaciones sigue siendo válido pero recogiendo el efecto del fraccionamiento en el usufructo y en el valor del título.
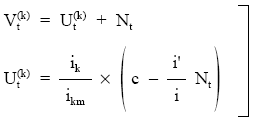
Al tratarse de un empréstito de cupón fraccionado, para resolverlo, obligatoriamente, se tendrá que calcular en primer lugar, y fuera del sistema, la nuda propiedad (Nt) aplicando la definición, esto es, actualizando los valores de reembolso futuros al tanto de mercado.
Del sistema se despejará siempre el usufructo y el valor.
EJEMPLO 30
Se emite el siguiente empréstito:
- Títulos emitidos: 10.000.
- Nominal título: 1.000 euros.
- Cupón semestral: 60 euros.
- Duración: 3 años.
- Sorteos anuales a la par.
- Anualidad comercial constante.
Se pide:
- Cuadro de amortización.
- Valor, usufructo y nuda propiedad a principios del año 2 a un tanto de mercado del 15% efectivo anual.
Solución:
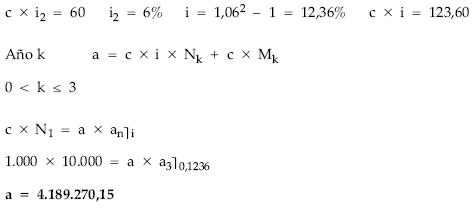
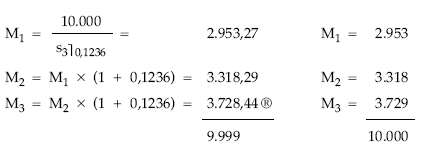
Cuadro de amortización
|
Año/Sem.
|
Títulos vivos
|
Título amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1.1.
1.2. 2.1. 2.2. 3.1. 3.2. |
10.000
10.000 7.047 7.047 3.729 3.729 |
–
2.953 – 3.318 – 3.729 |
–
2.953 2.953 6.271 6.271 10.000 |
600.000
600.000 422.820 422.820 223.740 223.740 |
–
2.953.000 – 3.318.000 – 3.729.000 |
600.000
3.553.000 422.820 3.740.820 223.740 3.952.740 |
Valor, usufructo y nuda propiedad transcurrido un año al tanto im = 15%
1.ª posibilidad: aplicando las definiciones

2.ª posibilidad: aplicando el sistema de ecuaciones
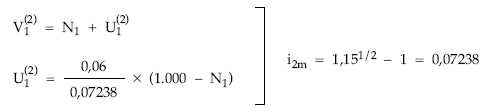
Aplicando la expresión de cálculo de la nuda propiedad:
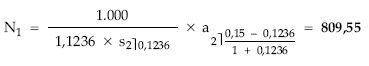
Del sistema se despeja el usufructo y a continuación el valor:

9.3.3. Empréstitos clase II, tipo I, normal
Empréstitos con término amortizativo constante y cupón acumulado en régimen de compuesta pagadero a los títulos que en cada sorteo resulten amortizados.
La estructura del término amortizativo es la siguiente:
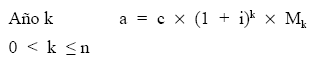
Se trata de realizar el cálculo del valor, usufructo y nuda propiedad de un título procedente de este empréstito en un momento cualquiera considerando los posibles escenarios antes comentados.
Caso 1: el título resultará amortizado en el momento k+t
Estamos suponiendo que se conoce con absoluta certeza el momento en que resultará amortizado el título estudiado.
Gráficamente el esquema de flujos pendientes desde la fecha de estudio (k) hasta el momento del sorteo (k+t):

Se calculará en primer lugar el valor y la nuda propiedad, aplicando la definición:
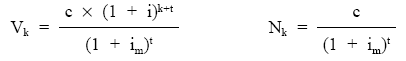
El usufructo resultará más práctico obtenerlo por diferencias entre los dos datos previamente obtenidos: Uk = Vk – Nk.
EJEMPLO 31
Se emite el siguiente empréstito:
- Títulos emitidos: 10.000.
- Nominal título: 1.000 euros.
- Cupón del 10% anual acumulable al momento del sorteo.
- Duración: 3 años.
- Anualidad comercial constante.
Se pide:
- Valor, usufructo y nuda propiedad en el origen de un título que resultará amortizado en el primer sorteo, siendo el tanto de mercado el 9%.
- Valor, usufructo y nuda propiedad en el origen de un título que resultará amortizado en el último sorteo, siendo el tanto de mercado el 9%.
Solución:
a) Si el título se amortiza en el primer año:
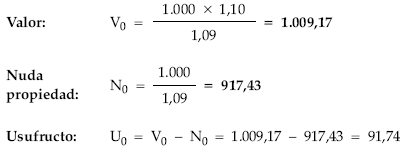
b) Si el título se amortiza en el tercer año:
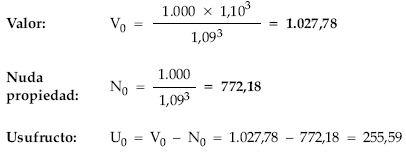
Caso 2: tomando como estimación la vida media del empréstito en la fecha de estudio
Se desconoce el momento en que resultará amortizado el título estudiado, por ello se toma como estimación la vida media calculada para todo el empréstito en la fecha donde se valora.
Gráficamente el esquema de flujos pendientes desde la fecha de estudio (k) hasta el momento del sorteo (k + Vm):

Se procederá de igual forma que en el caso anterior, pero tomando como horizonte temporal la vida media del empréstito.
Caso 3: considerando valores medios
En los dos casos anteriores, bien conociendo la fecha del sorteo bien tomando como horizonte de estudio la vida media del empréstito, se considera únicamente el título objeto de valoración. Ahora, por el contrario, se trabaja con el conjunto de títulos vivos en la fecha de estudio del empréstito, para, después, estimar el valor medio de cada uno de ellos.
El esquema de flujos pendientes del empréstito en su conjunto es el siguiente:
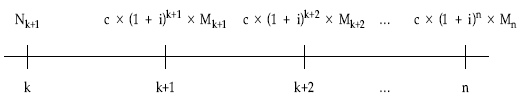
Aplicando las definiciones de usufructo, nuda propiedad y valor, en este caso aplicados para el conjunto del empréstito (valores totales o globales):
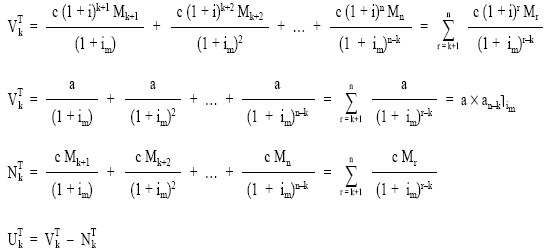
Estos valores globales se repartirán entre el número de títulos vivos en la fecha de estudio (Nk+1), para obtener los valores medios por título de usufructo, nuda propiedad y valor:
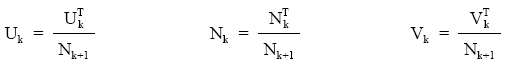
No obstante, este proceso de cálculo exige conocer los títulos amortizados en cada momento desde la fecha de estudio hasta el final del empréstito y las cantidades a pagar a cada uno de ellos en concepto de amortización y cupón acumulado.
Un sistema alternativo sería el siguiente:
• En primer lugar se calcula el valor medio de un título:
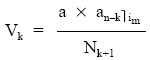
• A continuación se calcula la nuda propiedad, con la siguiente expresión:
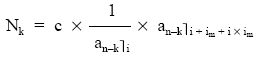
• Finalmente, se despeja el usufructo:
Uk = Vk – Nk
EJEMPLO 32
Se emite el siguiente empréstito:
- Títulos emitidos: 10.000.
- Nominal título: 1.000 euros.
- Cupón del 10% anual acumulable al momento del sorteo.
- Duración: 3 años.
- Anualidad comercial constante.
Se pide:
- Cuadro de amortización.
- Valor, usufructo y nuda propiedad en el origen a un tanto de mercado del 12% efectivo anual.
Solución:

Cuadro de amortización
|
Año
|
Títulos vivos
|
Título amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 |
10.000
6.344 3.021 |
3.656
3.323 3.021 |
3.656
6.979 10.000 |
365.600
697.830 999.951 |
3.656.000
3.323.000 3.021.000 |
4.021.600
4.020.830 4.020.951 |
Valor, usufructo y nuda propiedad en el origen al tanto im = 12%
1.ª posibilidad: aplicando las definiciones
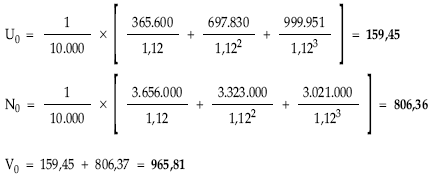
2.ª posibilidad: calculando el valor medio y a continuación la nuda propiedad con las expresiones abreviadas
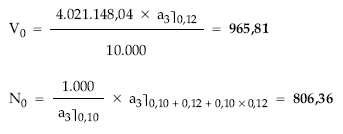
Finalmente se despeja el usufructo:
U0 = V0 – N0 = 159,45
9.3.4. Valor, usufructo y nuda propiedad en una fracción de período
Las expresiones anteriores se pueden aplicar para valoraciones efectuadas en momentos donde tiene lugar amortización de títulos (final de período –año–). Si el cálculo se realizará en cualquier otro momento de tiempo las definiciones siguen siendo válidas (y, por tanto, se pueden seguir aplicando) pero el sistema práctico de ecuaciones no se podría aplicar directamente.
En este caso con el sistema de ecuaciones se realizarán los cálculos a principios del período y después capitalizaremos hasta la fecha en la que se piden los valores. Esta capitalización se debe efectuar en régimen de compuesta y al tanto de mercado (im).
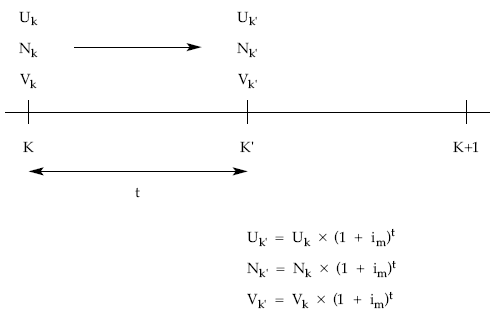
EJEMPLO 33
Se emite el siguiente empréstito:
- Títulos emitidos: 20.000.
- Nominal título: 1.000 euros.
- Cupón anual: 50 euros.
- Prima de amortización: 200 euros.
- Duración: 4 años.
- Gastos de administración del 1‰ de las cantidades pagadas a los obligacionistas.
- Anualidad comercial constante.
Se pide:
- Cuadro de amortización.
- Valor, usufructo y nuda propiedad transcurridos dos años desde la emisión a un tanto de mercado del 7% efectivo anual
- Valor, usufructo y nuda propiedad transcurridos dos años y tres meses desde la emisión a un tanto de mercado del 7% efectivo anual.
Solución:
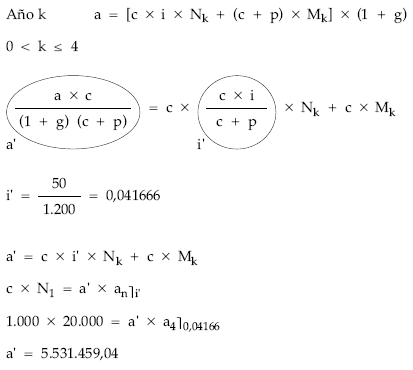
de donde:
a = 6.644.388,60
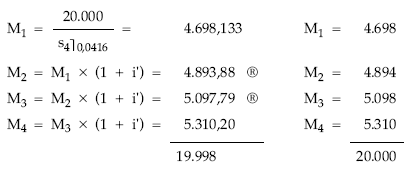
Cuadro de amortización
|
Año
|
Títulos vivos
|
Título amortiz.
|
Total tít. amort.
|
Intereses
|
Amortiz.
|
Gastos Admón.
|
Término amortizativo
|
|
1
2 3 4 |
20.000
15.302 10.408 5.310 |
4.698
4.894 5.098 5.310 |
4.698
9.592 14.698 20.000 |
1.000.000
765.100 520.400 265.500 |
5.637.600
5.872.800 6.117.600 6.372.000 |
6.637,6
6.637,9 6.638,0 6.637,5 |
6.644.237,6
6.644.537,9 6.644.638,0 6.644.137,5 |
Valor, usufructo y nuda propiedad en 2, al tanto im = 7 % (aplicando las definiciones)
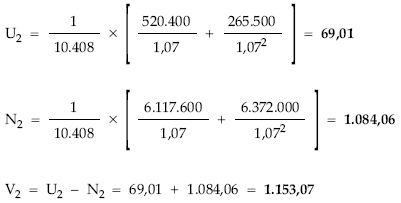
Los mismos resultados se habrían obtenido aplicando el sistema de ecuaciones.
Valor, usufructo y nuda propiedad transcurridos 2 años y 3 meses, al tanto im = 7%, (aplicando las definiciones)
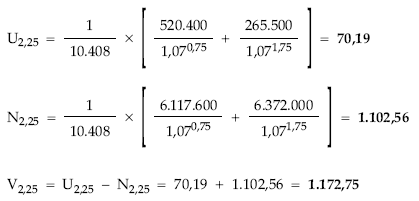
En este caso, para valorar en una fracción de período, el sistema de ecuaciones no se puede aplicar directamente. Habrá que valorar en el momento 2 (V2, U2 y N2) y después capitalizar 3 meses al tanto de mercado. Así, utilizando los resultados del punto anterior se realizarán finalmente los siguientes cálculos:
V2,25 = V2 x 1,070,25 = 1.153,04 x 1,070,25 = 1.172,74
U2,25 = U2 x 1,070,25 = 69,01 x 1,070,25 = 70,22
N2,25 = N2 x 1,070,25 = 1.084,06 x 1,070,25 = 1.102,53
| Nota: las pequeñas diferencias que surgen entre los diferentes métodos se deben al error de aproximación que se comete tanto en uno como en otro. |




