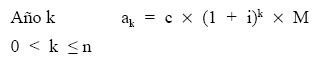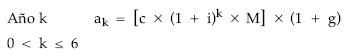En este tipo de empréstito, el emisor se compromete a amortizar el mismo número de títulos en cada sorteo a lo largo del tiempo que dure la operación.
7.1.1. Pasos a seguir
Lo más fácil será calcular el número de títulos amortizados en cada sorteo, para posteriormente ver qué se les ha de pagar. A continuación, se determinará el importe total a desembolsar por parte del emisor en cada período (término amortizativo).
7.1.1.1. Cálculo del número de títulos amortizados en cada sorteo (M)
Se parte de la igualdad entre los títulos inicialmente emitidos y los títulos que se amortizarán a lo largo de la vida del empréstito.
N1 = M1 + M2 + M3 + … + Mn = M x n
de donde se obtiene:
N1
M = —–
n
7.1.1.2. Cálculo del total de títulos amortizados después de k períodos (mk)
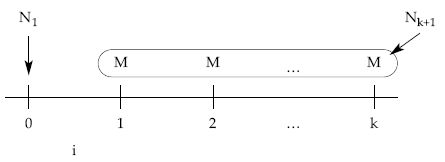
Si se conocen los títulos que se amortizan en cada sorteo, el total amortizado hasta una fecha dada será la suma aritmética de los títulos sorteados en ese intervalo.
mk = M1 + M2 + … + Mk = M x k
7.1.1.3. Cálculo de los títulos en circulación a principios del período k+1 (Nk+1)
Se realizará a través de los títulos amortizados (pasados o futuros).
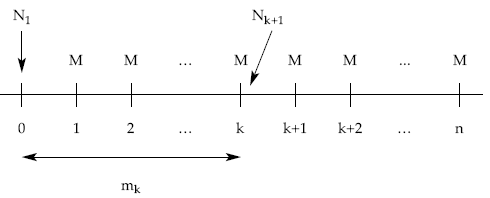
• Método retrospectivo: los títulos pendientes de amortizar serán los emitidos minorados en los ya amortizados hasta ese momento.
Nk+1 = N1 – mk = N1 – M x k
• Método prospectivo: los títulos pendientes de amortizar serán la suma aritmética de los que aún quedan pendientes de ser amortizados.
Nk+1 = (n – k) x M
7.1.1.4. Cálculo de los términos amortizativos: ley de recurrencia (ak)
Al mantenerse constante el número de títulos a los que hay que amortizar y el importe del cupón acumulado ir aumentando, los términos amortizativos necesariamente tendrán que ir creciendo.
La estructura de la anualidad quedará de la siguiente forma:
Para calcular el importe de los términos amortizativos planteamos dos alternativas:
A) 1.ª posibilidad: dando valores a k en la estructura del término amortizativo
| Período 1: | a1 = c x (1 + i) x M |
| Período 2: | a2 = c x (1 + i)2 x M |
| … |
B)
2.ª posibilidad: a través de la ley de recurrencia que siguen los términos amortizativos
Se calcula el primer término y el resto se obtienen a través de la ley de recurrencia que siguen y que se obtendrá al relacionar, por cocientes, dos términos amortizativos consecutivos cualesquiera:
| Período k: | ak = c x (1 + i)k x M |
| Período k+1: | ak+1 = c x (1 + i)k+1 x M |
| ——————————— | |
| ak c x (1 + i)k x M ——– = ———————— ak+1 c x (1 + i)k+1 x M |
simplificando el segundo miembro:
ak 1
——- = ——–
ak+1 1 + i
finalmente, se obtiene:
ak+1 = ak x (1 + i)
lo que indica que los términos varían en progresión geométrica de razón (1 + i), por lo que todos los términos se pueden calcular a partir del primero de ellos, siguiendo la ley de recurrencia:
ak+1 = a1 x (1 + i)k
Si hay características comerciales, éstas sólo afectarían al cálculo de los términos amortizativos y, en consecuencia, a la ley de recurrencia que siguen. No se normaliza.
EJEMPLO 18
Se emite el siguiente empréstito:
- Títulos emitidos: 60.000.
- Nominal del título: 1.000 euros.
- Duración: 6 años.
- Los títulos se adquieren a la par.
- No abono de cupones anuales, acumulándose al momento del sorteo al 10% anual.
- Sorteos anuales, amortizándose el mismo número de títulos.
- Gastos de administración del 1‰ sobre las cantidades pagadas anualmente a los obligacionistas.
- Gastos iniciales a cargo del emisor de 10.000 euros.
Se pide:
Términos amortizativos del empréstito.
Solución:
El número de títulos a amortizar en cada sorteo es la sexta parte del total de títulos emitidos:
60.000
M1 = M2 = … = M6 = M = ———– = 10.000
6
La anualidad variable se destina a amortizar el mismo número de títulos, reembolsándoles el nominal y el cupón acumulado hasta el sorteo en compuesta, además de unos gastos de administración:
Para conocer la cuantía de los términos, basta con darle valores a la anualidad, según el período al que le queramos calcular la anualidad:
| Año 1: | a1 = c x (1 + i)1 x M x (1 + g) |
| a1 = 1.000 x 1,1 x 10.000 x 1,001 = 11.011.000 | |
| Año 2: | a2 = c x (1 + i)2 x M x (1 + g) |
| a2 = 1.000 x 1,12 x 10.000 x 1,001 = 12.112.100 | |
| Año 3: | a3 = c x (1 + i)3 x M x (1 + g) |
| a3 = 1.000 x 1,13 x 10.000 x 1,001 = 13.323.310 | |
| Año 4: | a4 = c x (1 + i)4 x M x (1 + g) |
| a4 = 1.000 x 1,14 x 10.000 x 1,001 = 14.655.641 | |
| Año 5: | a5 = c x (1 + i)5 x M x (1 + g) |
| a5 = 1.000 x 1,15 x 10.000 x 1,001 = 16.121.205,1 | |
| Año 6: | a6 = c x (1 + i)6 x M x (1 + g) |
| a6 = 1.000 x 1,16 x 10.000 x 1,001 = 17.733.325,6 |
También se podían haber calculado todas las anualidades a partir de la primera (a1), observando que varían en progresión geométrica de razón 1 + i.