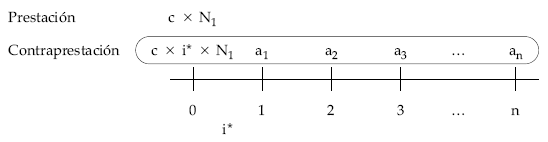
El esquema de la operación para un empréstito de N1 títulos emitidos, de nominal c, cupón periódico c x i* prepagable, con anualidades variables en progresión geométrica de razón conocida q y una duración de n períodos (años) es:
La estructura del término amortizativo será:
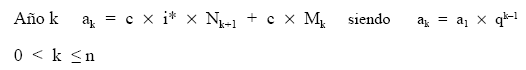
5.5.1. Pasos a seguir
5.5.1.1. Cálculo del primer término amortizativo (a1)
En el momento cero, inicio de la operación, la cantidad que recibe el emisor debe ser igual al valor actualizado, al tanto del préstamo i*, de los pagos que realizará hasta el final:
c x N1 = c x N1 x i* + a1 x (1 – i*) + a2 x (1 – i*)2 + a3 x (1 – i*)3 + … + an x (1 – i*)n
Simplificando en ambos miembros, pasando c x N1 x i* al primer miembro y poniendo todos los términos amortizativos en función del primero de ellos y la razón:
c x N1 – c x N1 x i* = a1 x (1 – i*) + a1 x q x (1 – i*)2 + a1 x q2 x (1 – i*)3 + … + a1 x qn-1 (1 – i*)n
sacando factor común a1 x (1 – i*):
c x N1 x (1 – i*) = a1 x (1 – i*) x [1 + q x (1 – i*) + q2 x (1 – i*)2 + … + qn-1 x (1 – i*)n-1]
En el segundo miembro el corchete no es más que una suma de n términos en progresión geométrica decreciente, que responde a la siguiente expresión:
a1 – an x r
S = —————
enable rich-textFormato de entrada Filtered HTML Etiquetas 1 – r?
siendo a1 el primer término de la suma, an el último de los términos y r la razón de la progresión.
Aplicando a este caso, se obtiene:
1 – qn-1 x (1 – i*)n-1 x q x (1 – i*)
c x N1 = a1 x ———————————————–
1 – q x (1 – i*)
1 – qn x (1 – i*)n
c x N1 = a1 x ————————
1 – q + q x i*
De donde se obtendrá el importe del primer término amortizativo (a1).
5.5.1.2. Cálculo de títulos amortizados: ley de recurrencia (Mk)
Para determinar el número de títulos a amortizar en cada sorteo se puede proceder de dos formas alternativas:
A) 1.ª posibilidad: dando valores a k en la estructura del término amortizativo
Se trata de saber el importe total pagado en cada momento (término amortizativo) y la parte destinada al pago de cupones. De esta forma, se sabrá cuánto queda para amortizar, determinándose así el número de títulos que podrán retirarse de la circulación en cada sorteo.
Para ello se comenzará por el último período, ya que el término amortizativo, al no tener que pagarse cupón, se destina íntegramente a amortizar, así:
| Período n: | an = c x Mn | an –> Mn =—— c |
| Período n–1: | an-1 = c x i* x Nn + c x Mn-1 | an–1 – c x i* x Nn –> Mn-1 = ———————– c |
| Siendo Nn = Mn, conocido | ||
| … |
Siguiendo de la misma manera se calcularán los títulos amortizados en cada sorteo.
B)
2.ª posibilidad: a través de la ley de recurrencia que siguen los títulos amortizados
La ley de recurrencia para obtener los títulos a amortizar en cada período se obtendrá por diferencias de dos términos amortizativos consecutivos cualesquiera, así:
| Período k: |
ak = c x i* x Nk+1 + c x Mk
|
| Período k+1: |
ak+1 = c x i* x Nk+2 + c x Mk+1
|
|
————————————————————————
|
|
|
ak – ak+1 = c x i* x (Nk+1 – Nk+2 + c x Mk – c x Mk+1
|
siendo Nk+1 – Nk+2 = Mk+1, queda:
ak x (1 – q) = c x i* x Mk+1 + c x Mk – c x Mk+1
dividiendo la expresión por c:
ak x (1 – q)
————— = i* x Mk+1+ Mk – Mk+1
c
de donde se obtiene:
ak x (1 – q)
Mk = Mk+1 x (1 – i*) + ——————
c
5.5.1.3. Cálculo del total de títulos amortizados (mk)
Conocer la totalidad de títulos amortizados en un momento de tiempo concreto se puede hacer de dos formas:
• Por diferencias, entre el número de títulos emitidos y los que aún están en circulación:
mk = N1 – Nk+1
• Por suma de los títulos amortizados hasta la fecha:
mk = M1 + M2 + … + Mk
5.5.1.4. Cálculo de títulos vivos a principio de cada período (Nk+1)
En todo momento de la vida del empréstito se cumple la igualdad entre el nominal del empréstito en ese momento y el valor actualizado de los pagos pendientes (incluido el pago del cupón situado en el momento de estudio que corresponde al primer período pendiente):
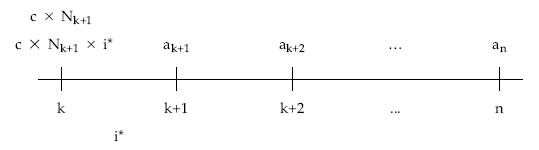
planteando la equivalencia en el momento k y simplificando:
c x Nk+1 = c x Nk+1 x i* + ak+1 x (1 – i*) + ak+2 x (1 – i*)2 + … + an x (1 – i*)n-k
pasando c x Nk+1 x i* al primer miembro y sacando factor común ak+1 x (1 – i*):
c x Nk+1 (1 – i*) = ak+1 x (1 – i*) x [1 + q (1 – i*) + q2 (1 – i*)2 + … + qn-k-1 (1 – i*)n-k-1]
dividiendo por 1 – i*:
c x Nk+1 x (1 – i*) = ak+1 x (1 – i*) [1 + q (1 – i*) + q2 (1 – i*)2 + … + qn-k-1 (1 – i*)n-k-1]
En el segundo miembro el corchete es la suma de n–k términos en progresión geométrica decreciente, por tanto, y simplificando, queda la siguiente expresión:
1 – qn-k x (1 – i*)n-k
c x Nk+1 = ak+1 x —————————-
1 – q + q x i*
De donde se obtendrá el número de títulos en circulación (Nk+1).
Hay que observar que la expresión obtenida es idéntica a la obtenida en el primer paso (para calcular la anualidad), variando la fecha donde están planteadas (una en 0 y otra en k).
5.5.1.5. Cálculo del importe a pagar de cupones en el momento k
Los cupones de cualquier período se calcularán a partir de los títulos en circulación a principios de ese período, a los que se les entregará el cupón acordado (c x i*), pero el cobro/pago se realizará a principios de ese período. Por tanto en k, principios del período k+1, se pagará el cupón correspondiente al período k+1.
En el momento k: c x i* x Nk+1




