La dificultad en este caso viene dada como consecuencia de la normalización, que origina unas anualidades normalizadas y unos tantos normalizados variables sin ninguna ley matemática.
En su resolución no podrá aplicarse ninguna de las expresiones válidas para empréstitos clase I, tipo I. Será preciso calcular en primer lugar la anualidad teórica para, a partir de ella, calcular el resto de datos.
El cálculo de la anualidad se hará planteando (como siempre) la equivalencia financiera en el origen entre el nominal del empréstito y las anualidades normalizadas actualizadas a los tantos normalizados vigentes en cada momento. En este caso, como consecuencia de las primas de amortización variables, tanto las anualidades normalizadas como los tantos normalizados no seguirán ningún tipo de ley (serán aleatorios), por lo tanto no se podrá utilizar en la actualización ni rentas ni sumatorios: habrá que desplazar uno a uno cada término.
EJEMPLO 13
Se emite el siguiente empréstito:
- Títulos emitidos: 100.000.
- Nominal del título: 1.000 euros.
- Duración: 4 años.
- Cupón anual: 120 euros.
- Sorteos anuales, amortizándose los títulos cada año al 110%, 120%, 130% y 150%, respectivamente.
- Anualidad comercial constante.
Se pide:
- Anualidad.
- Cuadro de amortización.
Solución:
La anualidad constante se destina a pagar un cupón periódico constante a los títulos en circulación y a amortizar los títulos con primas de amortización variables, sin que entre ellas haya ninguna ley matemática.
Pasos a seguir:
1. Estructura de la anualidad teórica
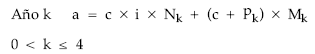
2. Normalización
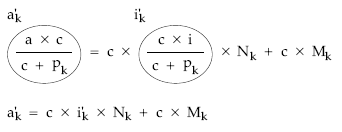
dando valores a k, para los diferentes años de vida de la operación resulta:
| k = 1 | a x c a’1 = ————- c + P1 |
c x i 120 i’1 = ———- = ———- = 0,1091 c + P1 1.100 |
| k = 2 | a x c a’2 = ———— c + P2 |
c x i 120 i’2 = ———- = ———- = 0,10 c + P2 1.200 |
| k = 3 | a x c a’3 = ———— c + P3 |
c x i 120 i’3 = ———- = ———- = 0,0923 c + P3 1.300 |
| k = 4 | a x c a’4 = ———— c + P4 |
c x i 120 i’4 = ———- = ———- = 0,08 c + P4 1.500 |
donde todo es conocido salvo la anualidad a.
3. Planteamiento de la equivalencia entre el nominal y las anualidades teóricas normalizadas actualizando término a término, al tanto vigente en cada momento
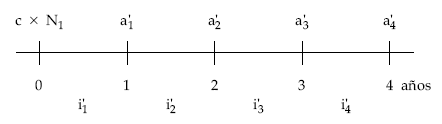
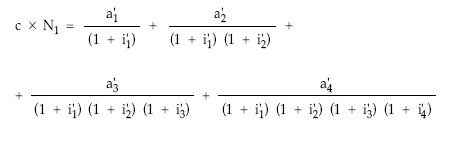
4. Sustitución de las anualidades y tantos normalizados por los valores obtenidos en la normalización
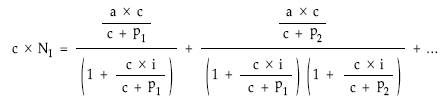
5. Sustitución en la expresión por valores numéricos y despeje de a
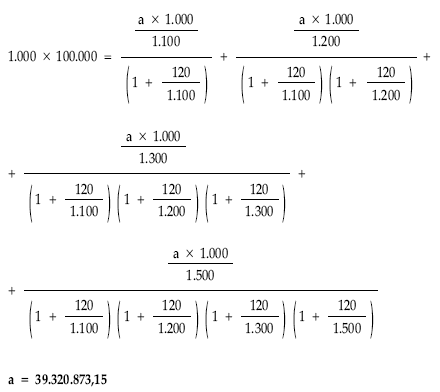
Cuadro de amortización: cálculo de títulos amortizados
1.ª posibilidad: a través de anualidad previamente calculada
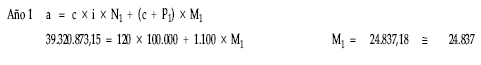
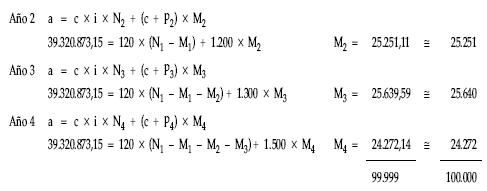
2.ª posibilidad: a través de la ley de recurrencia que sigue
La ley de recurrencia se obtiene al relacionar, por diferencias, las anualidades de dos períodos consecutivos cualesquiera, así:
| Período k: |
a = c x i x Nk + ck x Mk
|
siendo: ck = c + pk |
| Período k+1: |
a = c x i x Nk+1 + ck+1 x Mk+1
|
siendo: ck+1 = c + pk+1 |
|
———————————————————————
|
||
|
a – a = c x i x (Nk – Nk+1) + ck x Mk – ck+1 x Mk+1
|
||
simplificando ambos miembros, sabiendo que Nk – Nk+1 = Mk:
0 = c x i x Mk + ck x Mk – ck+1 x k+1
de donde se obtiene:
c x i + ck
Mk+1 = Mk x ————
ck+1
dando valores a k en la expresión anterior tendremos:
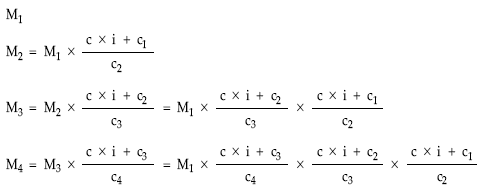
Para obtener M1, se tendrá en cuenta que se cumple la siguiente igualdad:
N1 = M1 + M2 + M3 + M4
Sustituyendo en el segundo miembro conseguiremos dejar una ecuación que dependa de M1:
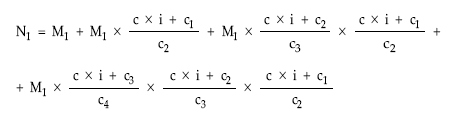
Finalmente se despeja M1:
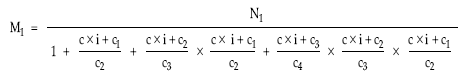
|
|
(1)
|
(2)
|
(3)
|
(4) = (1) x 120
|
(5) = 2 x (c + pk)
|
(6) = (4) + (5)
|
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 4 |
100.000
75.163 49.912 24.272 |
24.837
25.251 25.640 24.272 |
24.837
50.088 75.728 100.000 |
12.000.000
9.019.560 5.989.440 2.912.640 |
27.320.700
30.301.200 3.332.000 36.408.000 |
39.320.700
39.320.760 39.321.440 39.320.640 |




