La problemática de este tipo de empréstitos es la misma que la comentada cuando el término amortizativo es variable en progresión geométrica con características comerciales. Por tanto, la manera de proceder es la misma que la desarrollada en aquel caso.
EJEMPLO 10
Se emite el siguiente empréstito:
- Títulos emitidos: 100.000.
- Nominal del título: 1.000 euros.
- Duración: 4 años.
- Cupón anual: 125 euros.
- Sorteos anuales, amortizándose los títulos con prima de 200 euros.
- Anualidades comerciales variables en progresión aritmética de razón: 500.000 euros/año.
Se pide:
- Anualidad del tercer año.
- Cuadro de amortización
Solución:
Es un empréstito de cupón periódico constante y anualidad variable en progresión aritmética de razón 500.000 euros, con prima de amortización constante; los pasos a seguir son:
- Estructura de la anualidad teórica
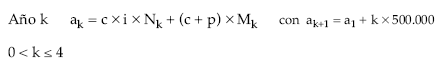
- Normalización
ak i
——– = c x ——– x Nk + Mk
c + p c + pak x c c x i
——– = c x ——– x Nk + c x Mk
c + p c + pSiendo:
c x ak c x i 125
a’ = ———- i’ = ——— = —————— = 0,10416666
c + p c + p 1.000 + 200Resulta el empréstito normalizado:
a’k = c x i’ x Nk + c x Mk
Gráficamente:
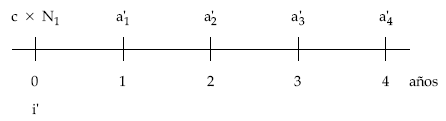
- Planteamiento de la equivalencia entre el nominal del empréstito y las anualidades teóricas normalizadas trabajando con sumatorios
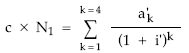
- Sustitución de la anualidad normalizada por el valor obtenido en la normalización
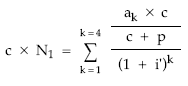
- Extracción del sumatorio de aquello que multiplique y/o divida en el numerador
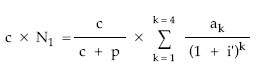
- Conversión de los sumatorios en sus respectivos valores actuales de renta
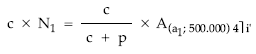
- Sustitución en la expresión por valores numéricos y despeje de a1
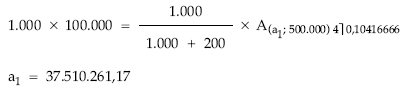
Anualidad del tercer año
a3 = a1 + 2 x 500.000 = 38.510.261,17
Cuadro de amortización
|
|
(1)
|
(2)
|
(3)
|
(4) = (1) x 125
|
(5) = (2) x 1.200
|
(6) = (4) + (5)
0 |
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 4 |
100.000
79.158 55.729 29.442 |
20.842
23.429 26.287 29.442 |
20.842
44.271 70.558 100.000 |
12.500.000
9.894.750 6.966.125 3.680.225 |
25.010.400
28.114.800 31.544.400 35.330.400 |
37.510.400
38.009.550 38.510.525 39.010.65 |
Cálculo de títulos amortizados
| Año 1: | a1 = c x i x N1 + (c + p) x M1 37.510.261,17 = 125 x 100.000 + 1.200 x M1 M1 = 20.841,88 |
| Año 2: | a2 = c x i x N2 + (c + p) x M2 38.010.261,17 = 125 x (N1 – M1) + 1.200 x M2 M2 = 23.429,58 |
| Año 3: | a3 = c x i x N3 + (c + p) x M3 38.510.261,17 = 125 x (N1 – M1 – M2) + 1.200 x M3 M3 = 26.286,83 |
| Año 4 | a4 = c x i x N4 + (c + p) x M4 39.010.261,17 = 125 x (N1 – M1 – M2 – M3) + 1.200 x M4 M4 = 29.441,7 |
Para el cálculo de Mk también se podía haber empleado la ley de recurrencia que siguen los títulos amortizados en este tipo de empréstitos.
| M1 = 20.841,88 ® | M1 = 20.842 |
| M2 = 23.429,58 | M2 = 23.429 |
| M3 = 26.286,83 ® | M3 = 26.287 |
| M4 = 29.441,71 ® | M44 = 29.442 |
| ————- 99.997 |
————- 100.000 |




