Todas las expresiones empleadas hasta ahora son válidas para empréstitos denominados normales o puros, es decir, aquellos en los que el término amortizativo se destina exclusivamente al pago de un cupón (constante) y a amortizar por el nominal a los títulos que corresponda.
No obstante, podemos encontrarnos con empréstitos en los que el emisor haya acordado retribuir adicionalmente a los obligacionistas (con primas de amortización y/o lotes) o bien incluyen gastos soportados por el emisor (gastos de administración). En estos casos, habrá que «preparar el empréstito» para que exista equilibrio financiero y así poder aplicar las expresiones anteriores.
Los pasos a seguir para trabajar con empréstitos de cupón periódico cuando tienen características comerciales son:
1.º Determinar la composición de la estructura de la anualidad siguiendo el siguiente orden:
Anualidad = Intereses + Amortización + Lotes + Gastos de administración
2.º Proceso de normalización: el objetivo final es dejar la estructura de partida en una equivalente en la que la anualidad se destine exclusivamente a pagar cupones y a amortizar por el nominal los títulos.
Las fases de la normalización son:
a) Pasar lo que no sea amortización ni cupón (lotes y gastos de administración) al primer miembro.
b) Si el valor de reembolso de los títulos es diferente del valor nominal de los títulos, dividir por el coeficiente de Mk toda la expresión.
c) Multiplicar por el nominal de los títulos toda la expresión.
El resultado de la normalización será una estructura pura (sin características comerciales):
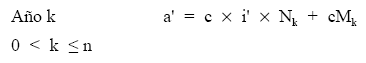
donde:
a’: es la anualidad normalizada.
i’: es el tanto normalizado.
3.º Las expresiones, fórmulas y reglas de cálculo de anualidad, títulos vivos, amortizados y total de amortizados, comentadas para el empréstito puro ahora son válidas pero cambiando a por a’ e i por i’.
No obstante, hay que tener en cuenta que existen características comerciales que aunque existan en el empréstito no afectan a la estructura de la anualidad y, por tanto, no precisan normalización: es el caso de la prima de emisión y los gastos de emisión. Además, la presencia de estas dos características no afecta al cálculo de la anualidad ni al cuadro de la operación.
EJEMPLO 3
Se emite el siguiente empréstito:
- Títulos emitidos: 1.000.
- Nominal título: 1.000 euros.
- Interés anual: 6%.
- Duración: 4 años.
- Amortización: 1.200 euros.
- Anualidad constante.
Se pide:
- Cálculo de la anualidad.
- Construir el cuadro de amortización.
Solución:
Cálculo de la anualidad
Se trata de un empréstito de cupón periódico constante y anualidad constante, con una prima de reembolso de 200 euros por título. La estructura de la anualidad será:
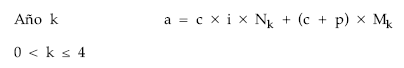
Como presenta características comerciales habrá que normalizar. Los pasos a seguir son:
• Dividir por el coeficiente de Mk:
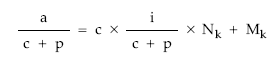
• Multiplicar por el nominal del título:
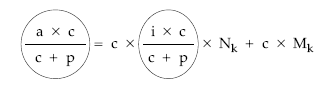
• Haciendo los siguientes cambios:
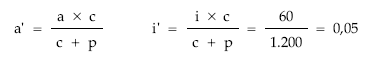
La estructura de la anualidad queda:
a’ = c x i’ x Nk + c x Mk
Estructura normal, a la que se puede aplicar las expresiones demostradas anteriormente para empréstitos clase I, tipo I, puros.
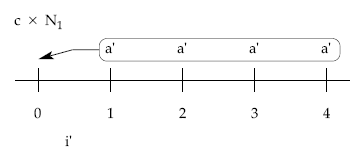
Planteando la equivalencia en origen:
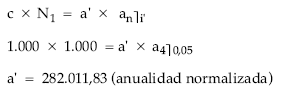
teniendo en cuenta el valor de a’ y deshaciendo el cambio de variable efectuado en la normalización obtendremos finalmente la anualidad teórica buscada:
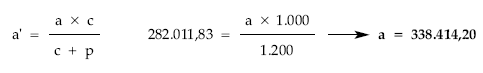
Cálculo de los títulos amortizados:

Cuadro de amortización
|
|
(1)
|
(2)
|
(3)
|
(4) = (1) x 60
|
(5) = (2) x 1.200
|
(6) = (4) + (5)
|
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 4 |
1.000
768 524 268 |
232
244 256 268 |
232
476 732 1.000 |
60.000
46.080 31.440 16.080 |
278.400
292.800 307.200 321.600 |
338.400
338.880 338.640 337.680 |
EJEMPLO 4
Se emite el siguiente empréstito:
- Títulos emitidos: 1.000.
- Nominal título: 1.000 euros.
- Interés anual: 5%.
- Duración: 3 años.
- Los títulos amortizados pierden el último cupón.
- Anualidad constante.
Se pide:
- Anualidad del empréstito.
- Cuadro de amortización.
Solución:
Cálculo de la anualidad
Se trata de un empréstito de cupón periódico constante y anualidad constante, con amortización seca (pérdida del último cupón de los títulos que resulten amortizados). La estructura de la anualidad será:
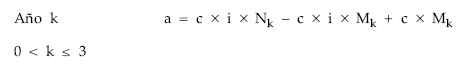
Como presenta características comerciales habrá que normalizar. Los pasos a seguir son:
• Sacar factor común Mk:
a = c x i x Nk + (c – c x i) x Mk
Con el fin de que el segundo miembro de la igualdad tenga dos términos, uno en función de Nk y otro en función de Mk.
• Dividir por el coeficiente de Mk:
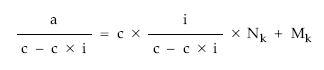
• Multiplicar por el nominal del título:
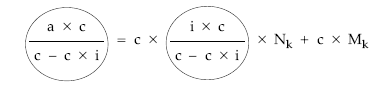
• Haciendo los siguientes cambios:
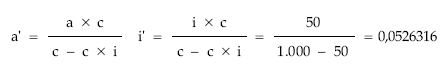
La estructura de la anualidad quedará:
a’ = c x i’ x Nk + c x Mk
estructura normal, a la que se pueden aplicar las expresiones demostradas anteriormente para empréstitos clase I, tipo I, puros.
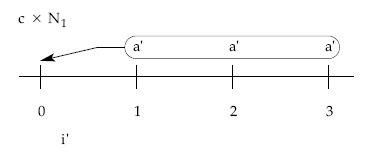
Planteando la equivalencia en origen:
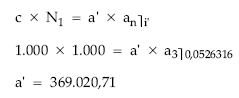
teniendo en cuenta el valor de a’, obtendremos finalmente a:
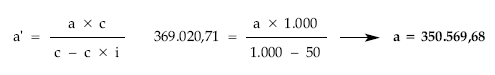
Cálculo de los títulos amortizados
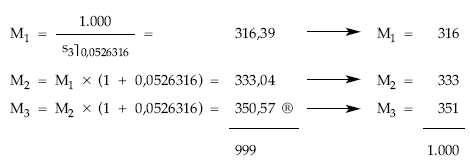
Cuadro de amortización
|
|
(1)
|
(2)
|
(3)
|
(4) = [(1) – (2)] x 50
|
(5) = (2) x 1.000
|
(6) = (4) + (5)
|
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 |
1.000
684 351 |
316
333 351 |
316
649 1.000 |
34.200
17.550 |
316.000
333.000 351.000 |
350.200
350.550 351.000 |
(4) Los intereses los cobrarán los títulos en circulación durante el año, salvo los que resulten amortizados al final del mismo: Nk – Mk.
Año 1: 1.000 – 316 = 684 684 x 50 = 34.200
Año 2: 684 – 333 = 351 351 x 50 = 17.550
Año 3: 351 – 351 = 0 0 x 50 = 0
Hay que observar que para el proceso de normalización la amortización seca se ha relacionado con el valor de reembolso, quedando la siguiente estructura:
a = c x i x Nk + (c – c x i) x Mk
No obstante, para construir el cuadro de amortización la amortización seca ha de aparecer como un menor pago de intereses y, por tanto, supondrá un menor pago de intereses, quedando la estructura de la anualidad de esta otra forma:
a = c x i x (Nk – Mk) + c x Mk
EJEMPLO 5
Se emite el siguiente empréstito:
- Títulos emitidos: 75.000.
- Nominal título: 1.000 euros.
- Cupón anual: 120 euros.
- Duración: 10 años.
- Sorteos anuales, amortizándose los títulos con prima de 200 euros.
- Los títulos se adquieren al 90%.
- Gastos iniciales de 500.000 euros a cargo del emisor.
- Gastos de administración del 1‰ sobre las cantidades pagadas anualmente a los obligacionistas.
- Anualidad constante.
Se pide:
- Anualidad del empréstito.
- Dos primeras líneas del cuadro de amortización.
Solución:
Cálculo de la anualidad
Es un empréstito de cupón periódico constante y anualidad constante, con prima de amortización y gastos de administración. Existen una prima de emisión y unos gastos iniciales pero no afectan al término amortizativo, por tanto, la estructura de la anualidad será:
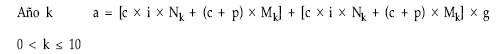
Sacando factor común el corchete:
![]()
Normalizando:
• Dividiendo por 1 + g toda la expresión:
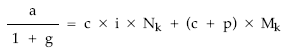
• Dividiendo por c + p toda la expresión:
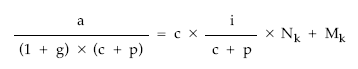
• Multiplicando por c toda la expresión:
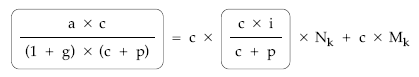
• Siendo:
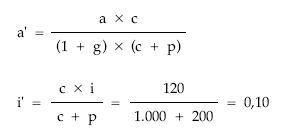
Resulta el empréstito normalizado:
a’ = c x i’ x Nk + c x Mk
estructura normal, a la que aplicaremos las expresiones de los empréstitos clase I, tipo I, puros.
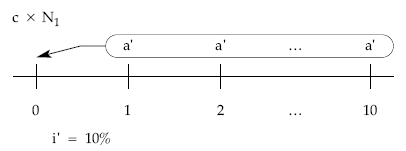
Planteando la equivalencia en origen:
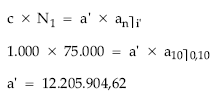
teniendo en cuenta el valor de a’, obtendremos finalmente a al deshacer el cambio de variable:

Cálculo del cuadro de amortización (2 líneas)
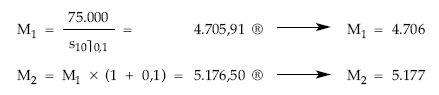
Al no conocer nada más que los títulos de dos sorteos se redondean los Mk atendiendo solamente al decimal (mayor o igual que cinco, por exceso y en caso contrario por defecto).
|
|
(1)
|
(2)
|
(3) = (1) x 20
|
(4) = (2) x 1.200
|
(5) = 1%o x [(3) + (4)]
|
(6) = (3) + (4) + (5)
|
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Intereses
|
Amortización
|
Gastos admón.
|
Término amortizativo
|
|
1
2 |
75.000
70.294 |
4.706
5.177 |
9.000.000
8.435.280 |
5.647.200
6.212.400 |
14.647,2
14.647,7 |
14.661.847,2
14.662.327,7 |




