Se parte de un empréstito que ya existe, cuyos títulos se encuentran en circulación y del que se conoce su sistema de amortización, es decir, cuántos títulos se van a amortizar en cada uno de los sorteos que aún quedan pendientes de realizar.
Lo que se pretende es la sustitución del plan de amortización inicialmente previsto por otro alternativo consistente en una amortización única de todos los títulos en circulación en el momento de estudio de una sola vez, obligándose a que ambos sistemas de amortización resulten equivalentes. El momento donde tendrá que efectuarse ese sorteo único que consiga la equivalencia financiera es lo que se denomina vida financiera del empréstito.
El estudio de equivalencia se efectuará en el momento donde se plantea la sustitución (k) valorándose las dos alternativas al tanto de mercado vigente en ese momento (im).
Caso 1: empréstito clase I, tipo I
La estructura del término amortizativo será la siguiente, para el caso de no tener características comerciales:
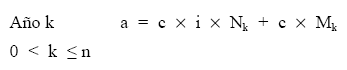
Situados a principios de k+1 el esquema de flujos futuros del empréstito, de acuerdo con el plan de reembolso inicialmente previsto, es el siguiente:
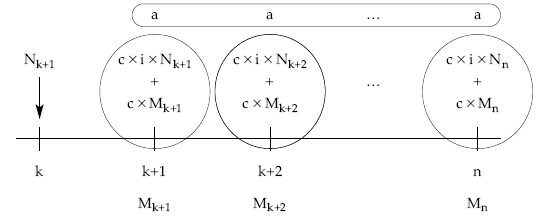
El sistema de amortización alternativo supone pagar periódicamente cupones a todos los títulos vivos en la fecha de estudio y amortizarlos todos de una sola vez en un momento futuro desconocido (la vida matemática). El esquema de flujos de caja del nuevo empréstito es el siguiente:
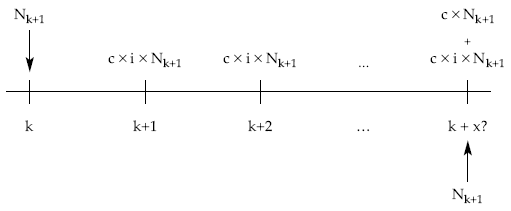
Valorando al tanto im en k las dos alternativas e igualándolas:
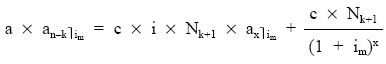
siendo X = vida financiera, la incógnita a despejar.
De igual manera que se ha trabajado con el empréstito en su conjunto, se podría realizar el estudio considerando solamente los cupones o los valores de reembolso.
1.º Considerando sólo el pago de cupones: vida financiera de los intereses (X1)
Se valoran en el momento k, por una parte los pagos de cupones que se realizarán en el futuro de acuerdo con el plan de amortización inicial y, por otra parte, los cupones que se pagarán caso de amortizar todos los títulos de una sola vez en X1. El resultado de igualar ambas corrientes de pagos será:
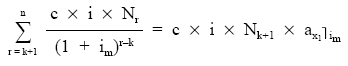
A continuación, se pasará Nk+1 al primer miembro de la ecuación, con lo que se obtiene la definición de usufructo medio del empréstito en ese momento (Uk).
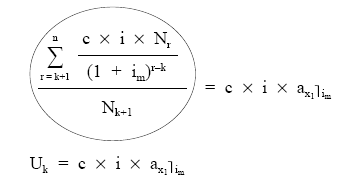
siendo X1 = vida financiera de los intereses, la incógnita a despejar.
2.º Considerando sólo el valor de reembolso: vida financiera de los valores de reembolso (X2)
Se valoran en el momento k, por una parte, los valores de reembolso que se realizarán en el futuro de acuerdo con el plan de amortización inicial y, por otra parte, el resultado de amortizar todos los títulos de una sola vez en X2 (desconocido). El resultado de igualar ambas corrientes de pagos será:
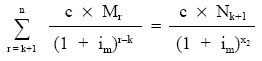
A continuación, se pasará Nk+1 al primer miembro de la ecuación, con lo que se obtiene la definición de nuda propiedad media del empréstito en ese momento (Nk).
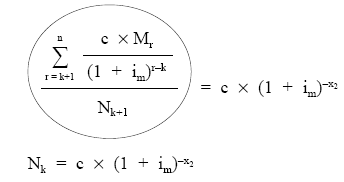
siendo X1 = vida financiera de los intereses, la incógnita a despejar.
Si el valor de reembolso se mantiene constante se cumple X = X1 = X2, lo que implica la existencia de una vida financiera única.
EJEMPLO 34
Se emite el siguiente empréstito:
- Títulos emitidos: 20.000.
- Nominal título: 1.000 euros.
- Cupón anual: 130 euros.
- Duración: 4 años.
- Prima de reembolso: 300 euros.
- Anualidad comercial constante.
Se pide:
- Cuadro de amortización.
- Vida financiera en el origen a un tanto de mercado del 8% efectivo anual.
Solución:
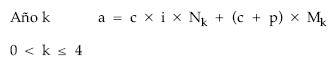
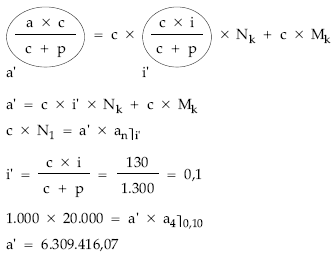
de donde:
a = 8.202.240,90
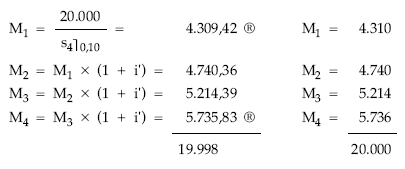
Cuadro de amortización
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 4 |
20.000
15.690 10.950 5.736 |
4.310
4.740 5.214 5.736 |
4.310
9.050 14.264 20.000 |
2.600.000
2.069.700 1.423.500 745.680 |
5.603.000
6.162.000 6.778.200 7.456.800 |
8.203.000
8.231.700 8.201.700 8.202.480 |
Vida financiera en el origen a un tanto de mercado del 8%
1.ª posibilidad: considerando todos los flujos del empréstito
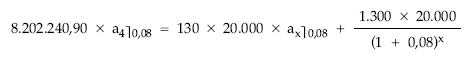
Vida financiera = X = 2,5709 años
2.ª posibilidad: considerando solamente los intereses del empréstito (usufructo)
Previamente se deberá calcular el usufructo medio de un título en la fecha donde se esté calculando la vida financiera (en este caso en el origen).
El usufructo medio en el origen es U0 = 291,712.
A continuación, se plantea la ecuación siguiente:
![]()
El cálculo de X (vida financiera o matemática) se puede hacer tanteando, máquina financiera (se trata de un elemento de una renta), con tablas financieras de valor actuales unitarios o mediante logaritmos, para lo cual será preciso desarrollar el segundo miembro de la igualdad:
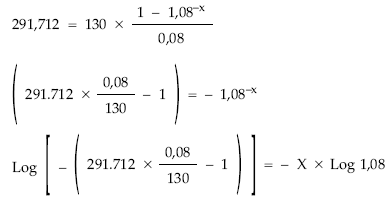
Vida financiera = X = 2,5709 años
3.ª posibilidad: considerando solamente los valores de reembolso del empréstito (nuda propiedad)
Previamente se deberá calcular la nuda propiedad media de un título en la fecha donde se esté calculando la vida financiera (en este caso en el origen).
La nuda propiedad media en el origen es N0 = 1.066,63.
A continuación, se plantea la ecuación siguiente:
1.300
1.066,63 = ———
1,08x
1.300
1,08x = ————-
1.066,63
Empleando logaritmos:
1.300
X x Log 1,08 = Log ————
1.066,63
Vida financiera = X = 2,5709 años
EJEMPLO 36
Se emite el siguiente empréstito:
- Títulos emitidos: 20.000.
- Nominal título: 1.000 euros.
- Cupón anual: 130 euros.
- Duración: 4 años.
- Prima de reembolso: 300 euros.
- Igual número de títulos amortizados cada año.
Se pide:
- Cuadro de amortización.
- Vida financiera en el origen a un tanto de mercado del 8%.
Solución:
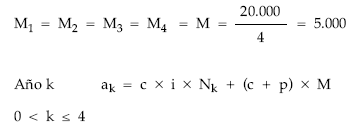
Cuadro de amortización
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Término
amortizativo |
|
1
2 3 4 |
20.000
15.000 10.000 5.000 |
5.000
5.000 5.000 5.000 |
5.000
10.000 15.000 20.000 |
2.600.000
1.950.000 1.300.000 650.000 |
6.500.000
6.500.000 6.500.000 6.500.000 |
9.100.000
8.450.000 7.800.000 7.150.000 |
Vida financiera en el origen a un tanto de mercado del 8%
1.ª posibilidad: considerando todos los flujos del empréstito
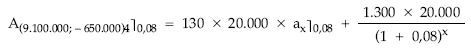
Vida financiera = X = 2,4519 años
2.ª posibilidad: considerando solamente los intereses del empréstito (usufructo)
Previamente se deberá calcular el usufructo medio de un título en la fecha donde se esté calculando la vida financiera (en este caso en el origen).
El usufructo medio en el origen es U0 = 279,45.
A continuación, se plantea la ecuación siguiente:
![]()
Mediante logaritmos:
Vida financiera = X = 2,4519 años
3.ª posibilidad: considerando solamente los valores de reembolso del empréstito (nuda propiedad)
Previamente se deberá calcular la nuda propiedad media de un título en la fecha donde se esté calculando la vida financiera (en este caso en el origen).
La nuda propiedad media en el origen es N0 = 1.076,44.
A continuación, se plantea la ecuación siguiente:
1.300
1.076,44 = ———
1,08x
Utilizando logaritmos:
Vida financiera = X = 2,4519 años
Caso 2: empréstito clase II, tipo I, puro.
La estructura del término amortizativo (anualidad) será la siguiente, para el caso de no tener características comerciales:
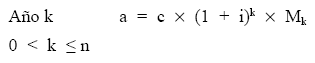
Situados a principios de k+1 el esquema de flujos futuros del empréstito, de acuerdo con el plan de reembolso inicialmente previsto, es el siguiente:
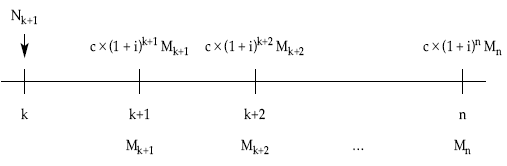
El resultado de actualizar todos estos flujos al momento k al tipo de mercado (im), quedaría:
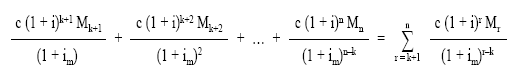
Por otra parte, el sistema de amortización alternativo supone la amortización de una sola vez de los títulos vivos en k en un momento futuro originando los siguientes flujos de caja:
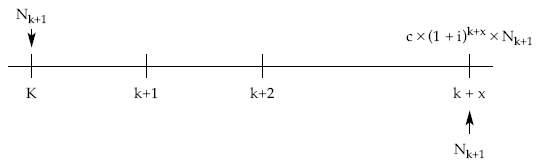
La actualización de ese único pago en el momento del estudio (k) al tanto de mercado resulta:
c x (1 + i)k+x x Nk+1
————————–
(1 + im)x
Finalmente, igualando las dos alternativas:
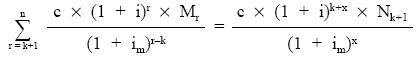
A continuación, se pasará Nk+1 al primer miembro de la ecuación, con lo que se obtiene la definición de valor medio del empréstito en ese momento (Vk).
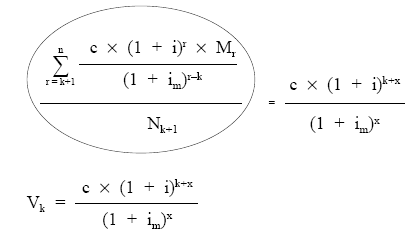
O de otra forma:
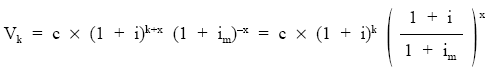
siendo X = vida financiera, la incógnita a despejar.
ANEXO I
Cálculo de la vida media en empréstitos clase I, tipo I, puro
Realizando el estudio en el origen:
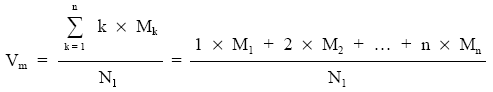
como: Mk = Nk – Nk+1
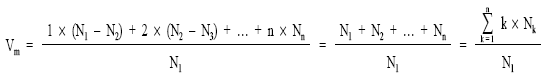
como:
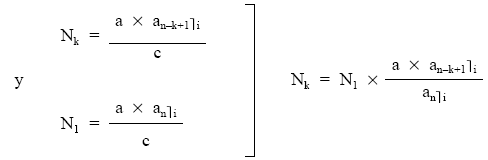
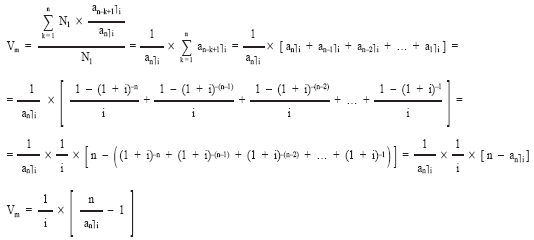
ANEXO II
Cálculo de la vida mediana en empréstitos clase I, tipo I, puro
Aplicando la definición en el origen:
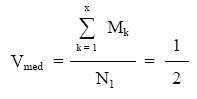
como:
∑ ![]()
y además se cumple:
![]()
sustituyendo:
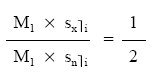
eliminando M1 y desarrollando el valor final de una renta unitaria pospagable:
(1 + i)x – 1
—————–
i 1
—————– = ——-
(1 + i)n – 1 2
—————–
i
eliminamos el i de ambos denominadores:
(1 + i)x – 1 1
—————- = ——
(1 + i)n – 1 2
reordenando la expresión:
(1 + i)n – 1
(1 + i)x – 1 = —————
2
resultando finalmente la expresión buscada:
(1 + i)n + 1
(1 + i)x = —————
2




