Al ser un préstamo fraccionado los intereses se harán efectivos fraccionadamente dentro del período de amortización, mientras que las cuotas de amortización no se fraccionan y se abonan al final del período.
Considerando que el importe del préstamo es C0, y el tipo de interés constante es ik, expresado en la unidad de tiempo en la que se pagan los intereses, durante n períodos, caben dos posibilidades de llevar a cabo el fraccionamiento en este tipo de préstamos:
- Resultando constante el término amortizativo único equivalente que se situaría en el momento de las amortizaciones.
- Siendo constante la cuantía total satisfecha en el momento de amortizar (tanto por amortización como por intereses).
9.2.1.
Resultando constante el término amortizativo único equivalente que se situaría en el momento de las amortizaciones
En este caso, al tratarse de un sistema francés y dado que el fraccionamiento sólo afecta a los intereses, se trata de calcular en primer lugar las cuotas de amortización (que se obtienen con las reglas vistas anteriormente para el caso del préstamo francés, sin fraccionamiento), a continuación los capitales pendientes y, finalmente, los intereses y términos amortizativos.
Pasos a seguir:
1.º A partir del tipo de interés de partida calcular el tanto efectivo equivalente expresado en la unidad de tiempo en la que se amortiza el capital.
i = (1 + ik)k – 1
2.º Cálculo de la primera cuota de amortización, siguiendo las fórmulas empleadas en el préstamo francés cuando no existe fraccionamiento de intereses, puesto que dicho fraccionamiento sólo afecta a los intereses pero no a las cuotas de amortización que se siguen calculando de la misma forma.
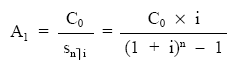
siendo n el número de cuotas de principal con las que amortizamos el préstamo.
3.º Cálculo del resto de cuotas de amortización, que variarán en progresión geométrica creciente de razón (1 + i).
At+1 = At x (1 + i) = A1 x (1 + i)t
4.º Cálculo del total amortizado, mt, por sumas parciales de las cuotas de amortización, que se pueden calcular una a una y sumándose posteriormente, o bien, se pueden sumar directamente a través de la ley que siguen:
![]()
5.º Cálculo del capital vivo, Ct, restando al capital pendiente del período anterior la cuota de amortización del período en curso o bien restando al importe del préstamo el total amortizado hasta el momento:
Ct = Ct-1 – At = C0 – mt
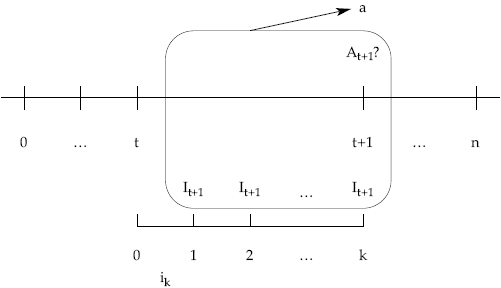
6.º Cálculo de las cuotas de interés, It+1, que se pagarán con la frecuencia acordada y siempre a partir del capital pendiente a principios del período a que se refiera empleando el tanto efectivo expresado en la unidad en la que se estén pagando los intereses (ik).
It+1 = Ct x ik
7.º Cálculo de los términos amortizativos, por suma de lo que en cada subperíodo se esté pagando: siempre intereses y en el último de cada período, además, cuota de amortización.
- Los primeros k–1 subperíodos (sólo intereses):
at, j = It+1
- El último subperíodo (interés y amortización):
at, k = It+1 + At
Otro camino alternativo, válido para este tipo de préstamos, consiste en calcular el término amortizativo anual equivalente para, a partir del mismo, calcular los capitales vivos, las cuotas de interés y finalmente las cuotas de amortización y los términos amortizativos en cada momento.
Pasos a seguir:
1.º A partir del tipo de interés de partida calcular el tanto efectivo equivalente expresado en la unidad de tiempo en la que se amortiza el capital.
i = (1 + ik)k – 1
2.º Cálculo del término amortizativo equivalente, siguiendo las fórmulas empleadas en el préstamo francés.
![]()
3.º Cálculo del capital pendiente a principios del período t + 1.
Método retrospectivo, a través de los términos amortizativos pasados.
![]()
Método prospectivo, a través de los términos amortizativos futuros.
![]()
4.º Cálculo de las cuotas de interés pagadas dentro del período t + 1.
Los intereses de cualquier subperíodo se calcularán a partir de la deuda pendiente a principios de ese período, al tanto efectivo fraccionado vigente durante el mismo.
It+1 = Ct x ik
5.º Cálculo de la cuota de amortización del período t + 1
Se debe mantener la equivalencia financiera entre el término amortizativo equivalente calculado inicialmente y los pagos que realmente tienen lugar dentro del período, las k cuotas de interés k-esimal y la cuota de amortización satisfecha a final del período. Por tanto, el término amortizativo equivalente, al final del período, debe coincidir con las cuotas de interés (conocidas) del período llevadas al final de dicho período más la cuota de amortización (que se desconoce). De esa equivalencia se obtendrá la cuota de amortización del período.
![]()
De donde se despejaría At+1.
El resto de cuotas de amortización se puede obtener de la misma forma, para cada período o bien, siguiendo la ley de recurrencia que mantienen (en progresión geométrica de razón 1 + i).
6.º Cálculo de los términos amortizativos, por suma de lo que en cada subperíodo se esté pagando: siempre intereses y en el último de cada período, además, cuota de amortización.
- Los primeros k–1 subperíodos (sólo intereses):
at, j = It+1
- El último subperíodo (intereses y amortización):
at, k = It+1 + At
EJEMPLO 10
Construir el cuadro de amortización del siguiente préstamo:
- Importe: 1.000.000 de euros.
- Duración: 3 años.
- Sistema francés:
– Cuotas de amortización anuales.
– Intereses semestrales al 5% efectivo semestral.
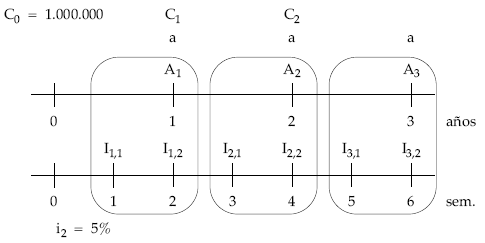
I1,1 = I1,2 = C0 x 0,05
I2,1 = I2,2 = C1 x 0,05
I3,1 = I3,2 = C2 x 0,05
i = 1,052 – 1 = 10,25%
|
|
(3)
|
(4)
|
(1)
|
(2)
|
(5)
|
|
Períodos
|
Capital
vivo |
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Términos amortizativos
|
|
1.1.
1.2. |
1.000.000,00
1.000.000,00 |
50.000,00
50.000,00 |
–
301.385,81 |
–
301.385,81 |
50.000,00
351.385,81 |
|
2.1.
2.2. |
698.614,19
698.614,19 |
34.930,71
34.930,71 |
–
332.277,86 |
301.385,81
633.663,67 |
34.930,71
367.208,57 |
|
3.1.
3.2. |
366.336,33
366.336,33 |
18.316,82
18.316,82 |
–
366.336,33 |
633.663,67
1.000.000,00 |
18.316,82
384.653,15 |
|
Total
|
|
206.495,06
|
1.000.000,00
|
|
1.206.495,06
|
Descripción de los pasos a seguir para construir el cuadro:
(1) Se calcula el importe de la primera cuota de amortización, a través de la fórmula prevista para calcular A1 en el préstamo francés, y, a partir de ella, todas las demás, multiplicando la cuota anterior por 1,1025.
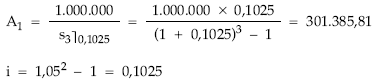
(2) Se calcula el total amortizado por sumas parciales de las cuotas de amortización practicadas hasta la fecha.
(3) La deuda pendiente se obtendrá de restar al capital a principios de cada período la cuota de amortización de ese mismo período, o bien, al importe del préstamo se le resta el total amortizado (2) ya acumulado.
(4) Las cuotas de interés se calculan sobre el capital pendiente a principios de cada período (3) al tanto efectivo semestral.
(5) El término amortizativo de cada período será la suma de las columnas (1) y (4).
9.2.2.
Siendo constante la cuantía satisfecha en el momento de amortizar (tanto por amortización como por intereses)
Pasos a seguir:
1.º Cálculo de la ley de recurrencia entre cuotas de amortización consecutivas, de forma que resulte constante la cuantía total pagada al final de cada período. Para ello obligamos a que el pago total a efectuar al final de dos períodos consecutivos cualesquiera coincida:
- Pago total al final del período t:
At + Ct-1 x ik
- Pago total al final del período t + 1:
At+1 + Ct x ik
Obligando a que sean iguales ambas cuantías, resulta:
At + Ct-1 x ik = At+1 + Ct x ik
Operando en la igualdad, pasando Ct x ik al primer miembro:
At + Ct-1 x ik – Ct x ik = At+1
Sacando factor común ik en el primer miembro:
At + (Ct-1 – Ct) x ik = At+1
Siendo:
Ct-1 – Ct = At
Resulta finalmente:
At + At x ik = At+1
De donde se obtiene:
At+1 = At x (1 + ik)
Siendo ik el tanto al que se va a calcular los intereses a pagar en cada subperíodo.
Al aplicar esta ley para cualesquiera dos períodos consecutivos, se observa que varían siguiendo una progresión geométrica de razón 1 + ik, por tanto, cualquier cuota se puede calcular a partir de la anterior, de la primera o de cualquiera conocida. Con carácter genérico, se pondrán en función de la primera –que es la más fácil de obtener–:
At+1 = A1 x (1 + ik)t
2.º Cálculo de la primera cuota de amortización a través de la siguiente expresión:
En todo préstamo se cumple que la suma aritmética de todas las cuotas de amortización es el importe del préstamo:
A1 + A2 + A3 + … + An = C0
Además, según la ley de recurrencia que siguen las cuotas de amortización, se pueden poner todas en función de la primera de ellas:
A1 + A1 (1 + ik) + A1 (1 + ik)2 + … + A1 (1 + ik)n-1 = C0
Simplificando la expresión:
A1 x [1 + (1 + ik) + (1 + ik)2 + … + (1 + ik)n-1] = C0
Siendo el corchete el valor final de una renta unitaria, pospagable e inmediata de n términos (el número de cuotas de amortización), al tanto ik al que se calculan las cuotas de interés, por tanto:
![]()
De donde:
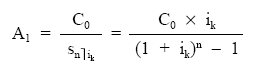
3.º Cálculo del resto de cuotas de amortización, que siguen como ley de recurrencia una progresión geométrica de razón (1 + ik).
A2 = A1 x (1 + ik)
A3 = A2 x (1 + ik) = A1 x (1 + ik)2
…
At+1 = At x (1 + ik) = A1 x (1 + ik)t
4.º Cálculo del total amortizado, mt, por sumas parciales de las cuotas de amortización, ya practicadas.
mt = A1 + A2 + … + At
5.º Cálculo del capital vivo, Ct , restando al capital pendiente del período anterior la cuota de amortización del período en curso o bien restando al importe del préstamo el total amortizado hasta el momento:
Ct = Ct-1 – At = C0 – mt
6.° Cálculo de la cuota de interés, It+1, que se pagará con la frecuencia acordada y siempre a partir del capital pendiente a principios del período a que se refiera empleando el tanto efectivo expresado en la unidad en la que se estén pagando los intereses (ik).
It+1 = Ct x ik
7.º Cálculo de los términos amortizativos, por suma de lo que en cada subperíodo se esté pagando: siempre intereses y en el último de cada período, además, cuota de amortización.
- Los primeros k–1 subperíodos (sólo intereses):
at, j = It+1
- El último subperíodo (interés y principal):
at, k = It+1 + At+1
EJEMPLO 11
Construir el cuadro de amortización del siguiente préstamo:
- Importe: 1.000.000 de euros.
- Duración: 3 años.
- Sistema francés:
– Cuotas de amortización anuales.
– Intereses semestrales al 5% efectivo semestral.
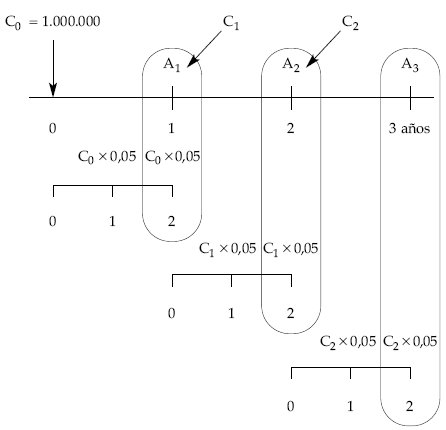
Se ha de cumplir:
A1 + C0 x 0,05 = A2 + C1 x 0,05 = A3 + C2 x 0,05
|
(3)
|
(4)
|
(1)
|
(2)
|
(5)
|
|
|
Períodos
|
Capital
vivo |
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Términos amortizativos
|
|
1.1.
1.2. |
1.000.000,00
1.000.000,00 |
50.000,00
50.000,00 |
–
317.208,56 |
–
317.208,56 |
50.000,00
367.208,56 |
|
2.1.
2.2. |
682.791,44
682.791,44 |
34.139,57
34.139,57 |
–
333.069,00 |
317.208,56
650.277,56 |
34.139,56
367.208,56 |
|
3.1.
3.2. |
349.722,44
349.722,44 |
17.486,12
17.486,12 |
–
349.722,44 |
650.277,56
1.000.000,00 |
17.486,12
367.208,56 |
|
Total
|
203.251,38
|
1.000.000,00
|
1.203.251,38
|
Descripción de los pasos a seguir para construir el cuadro:
(1) Se calcula el importe de la primera cuota de amortización, a través de la fórmula correspondiente, y, a partir de ella, todas las demás, multiplicando la cuota anterior por 1,05.
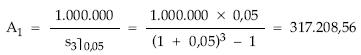
(2) Se calcula el total amortizado por sumas parciales de las cuotas de amortización practicadas hasta la fecha.
(3) La deuda pendiente se obtendrá de restar al capital a principios de cada período la cuota de amortización de ese mismo período, o bien, al importe del préstamo se le resta el total amortizado (2) ya acumulado.
(4) Las cuotas de interés se calculan sobre el capital pendiente a principios de cada período (3) al tanto efectivo semestral.
(5) El término amortizativo de cada período será la suma de las columnas (1) y (4).




