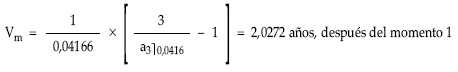Se define la vida media de un título como el tiempo que por término medio está en circulación ese título desde la fecha de estudio. Se trata del concepto de esperanza matemática de una variable (número de años en circulación), puesto que la variable es de tipo aleatorio (no se conoce el momento en que el título resultará amortizado).
En definitiva, la vida media resulta de multiplicar el número de años que un título puede estar en circulación, desde la fecha de estudio, por la probabilidad de que así ocurra:
Cuadro de trabajo si el estudio se realiza en el momento k:
|
SUCESOS
POSIBLES (momento del sorteo) |
X (n.º años en circulación)
|
PROBABILIDAD DEL SUCESO (Px)
|
X x Px
|
|
k+1
k+2 … n |
1
2 … n – k |
Mk+1/Nk+1
Mk+1/Nk+1 … Mn/Nk+1 |
1 x Mk+1/Nk+1
2 x Mk+1/Nk+1 … (n – k) n/Nk+1 |
Haciendo el estudio en el momento K, desde la emisión del empréstito, resulta:
Mk+1 Mk+2 Mn
Vm = 1 x ——– + 2 x ——— + … + (n – k) x ——–
Nk+1 Nk+1 Nk+1
De forma reducida:
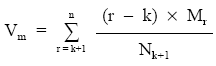
Si el estudio se hace en el origen (k = 0):
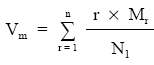
Expresiones válidas para cualquier empréstito, que tienen como principal inconveniente la necesidad de conocer el número de títulos en circulación en la fecha de estudio (Nk+1) así como el número de títulos a amortizar desde esa fecha hasta el final del empréstito (Mr).
No obstante, para empréstitos con anualidad constante y cupón periódico, constante y vencido (clase I, tipo I) se puede emplear la siguiente expresión simplificada (véase demostración en el anexo I al final del capítulo):
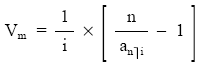
donde:
i Tanto del cupón del empréstito.
n Número de sorteos del empréstito.
método válido si el estudio se realiza en el origen. Para aplicar la fórmula en cualquier momento k, bastará con sustituir n (número de sorteos pendientes) por n–k (número de sorteos pendientes desde la fecha de estudio). Además, si el empréstito tuviera características comerciales, habría que normalizar y la expresión seguirá siendo válida pero cambiando i por i’ (tanto normalizado), resultando:
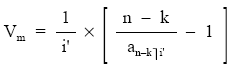
siendo:
i’: Tanto normalizado del empréstito.
n – k: Número de sorteos pendientes del empréstito.
EJEMPLO 3
Se emite el siguiente empréstito:
- Títulos emitidos: 20.000.
- Nominal título: 1.000 euros.
- Cupón anual: 50 euros.
- Duración: 4 años.
- Prima amortización: 200 euros.
- Anualidad constante.
Se pide:
- Cuadro de amortización.
- Vida media en el origen.
- Vida media en el momento 1.
Solución:
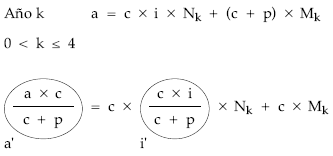
50
i’ = ——– = 0,04166
1.200
a’ = c x i’ x Nk + c x Mk
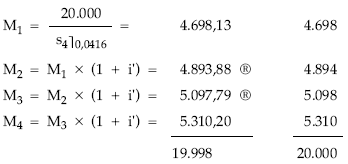
Planteando la equivalencia en el origen para calcular la anualidad:
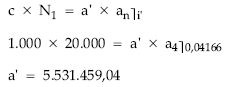
como:
a x c
a’ = ———
c + p
se podrá despejar la anualidad teórica:
a = 6.637.750,85
Cuadro de amortización
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Intereses
|
Amortización
|
Anualidad
práctica |
|
1
2 3 4 |
20.000
15.302 10.408 5.310 |
4.698
4.894 5.098 5.310 |
4.698
9.592 14.698 20.000 |
1.000.000
765.100 520.400 265.500 |
5.637.600
5.872.800 6.117.600 6.372.000 |
6.637.600
6.637.900 6.638.000 6.637.500 |
Vida media en el origen
1
Vm = ———– x [1 x 4.698 + 2 x 4.894 + 3 x 5.098 + 4 x 5.310] = 2,551 años
20.000
Otra posibilidad:
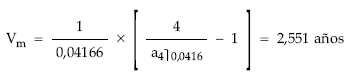
Vida media en el momento 1
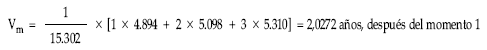
Otra posibilidad: