En este préstamo los intereses se harán efectivos fraccionadamente dentro del período de amortización, mientras que las cuotas de amortización constantes no se fraccionan y se abonan al final del período.
Considerando que el importe del préstamo es C0, amortizable en n pagos, con un tipo de interés constante i, expresado en la unidad en la que se amortiza el principal.
Por tanto, debe cumplirse que:
A1 = A2 = A3 = … = An = A
En primer lugar se calculará todo lo que tenga que ver con las cuotas de amortización, ya calculadas, a continuación los intereses y, finalmente, por suma, los términos amortizativos.
9.1.1. Cálculo de la cuota de amortización (A)
Sabiendo que la suma de todas las cuotas de principal es el importe del préstamo y que, además, éstas se mantienen constantes se debe cumplir:
C0 = A1 + A2 + A3 + … + An = A x n
de donde se obtiene:
C0
A = ——
n
9.1.2. Cálculo del total amortizado después de t períodos (mt)
Conociendo lo que se amortiza en cada momento (A), el total amortizado hasta una fecha será la suma aritmética de las cuotas ya efectuadas.
mt = A1 + A2 + … + At = A x t
9.1.3. Cálculo del capital vivo a principios del período t+1 (Ct)
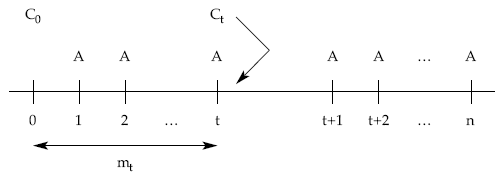
Se realizará a través de las cuotas de amortización (pasadas o futuras).
1.ª
posibilidad: por el método retrospectivo, el capital pendiente será el importe del préstamo disminuido en la totalidad de las cuotas de amortización ya practicadas
Ct = C0 – [A1 + A2 + … + At] = C0 – mt = C0 – A x t
2.ª
posibilidad: por el método prospectivo, el capital pendiente será la suma aritmética de las cuotas de amortización aún pendientes de realizar
Ct = At+1 + At+2 + … + An = (n – t) x A
9.1.4. Cálculo de las cuotas de intereses del período t+1
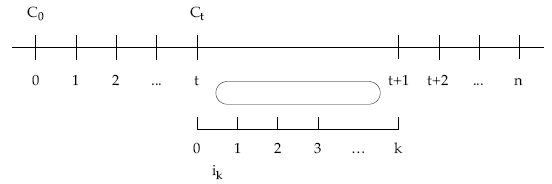
Los intereses de cualquier período se calcularán a partir de la deuda pendiente a principios de ese período (Ct), al tanto efectivo fraccionado (ik)vigente durante el mismo. Por tanto, dentro del período de amortización, habrá k pagos de intereses, cuyo importe se calcula así: It+1 = Ct x ik
9.1.5. Cálculo de los términos amortizativos (ak)
Los términos amortizativos se obtendrán finalmente como la suma de la cuota de interés y la cuota de amortización, cuando ésta tenga lugar (al final de cada período).
Así resulta para el período t:
- Los primeros k–1 subperíodos sólo incluye intereses:
at, j = It+1
- El último subperíodo, además de interés incluye la cuota de amortización del período:
at, k = It+1 + At
EJEMPLO 9
Construir el cuadro de amortización del siguiente préstamo:
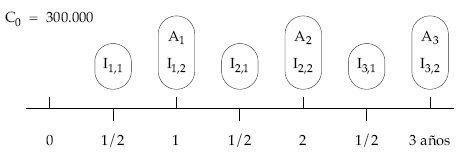
- Importe: 300.000 euros.
- Duración: 3 años.
- Cuotas de amortización anuales constantes.
- Intereses semestrales al 6% efectivo semestral.
|
|
(3)
|
(4)
|
(1)
|
(2)
|
(5)
|
|
Períodos
|
Capital
vivo |
Cuota de interés
|
Cuota de amortización
|
Total amortizado
|
Términos amortizativos
|
|
1.1.
1.2. |
300.000,00
300.000,00 |
18.000,00
18.000,00 |
–
100.000,00 |
–
100.000,00 |
18.000,00
118.000,00 |
|
2.1.
2.2. |
200.000,00
200.000,00 |
12.000,00
12.000,00 |
–
100.000,00 |
100.000,00
200.000,00 |
12.000,00
112.000,00 |
|
3.1.
3.2. |
100.000,00
100.000,00 |
6.000,00
6.000,00 |
–
100.000,00 |
200.000,00
300.000,00 |
6.000,00
106.000,00 |
|
Total
|
|
72.000,00
|
300.000,00
|
|
372.000,00
|
Descripción de los pasos a seguir para construir el cuadro:
(1) Se calcula la cuota de amortización a través del fraccionamiento del importe del préstamo en tres pagos iguales.
300.000
A = ————- = 100.000
3
(2) Se calcula el total amortizado por sumas parciales de las cuotas de amortización practicadas hasta la fecha.
(3) La deuda pendiente se obtendrá de restar al capital a principios de cada período la cuota de amortización de ese mismo período, o bien, al importe del préstamo se le resta el total amortizado (2) ya acumulado.
(4) Las cuotas de interés se calculan sobre el capital pendiente a principios de cada período (3) al tanto efectivo semestral.
(5) El término amortizativo de cada período será la suma de las columnas (1) y (4).




