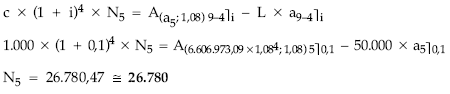Al igual que ocurría en empréstitos de cupón periódico con anualidades variables, puede ser que, como consecuencia de la normalización, lo que al principio era una anualidad variable en progresión geométrica con una determinada razón, resulte diferente porque varíe la razón o, incluso, porque ya no sigan esa ley geométrica, pudiendo incluso pasar a ser aleatorios los términos normalizados.
Para evitar este tipo de problemas procederemos siempre de la misma forma (aun cuando las características no afecten a la progresión geométrica de partida), e igual a como se hace en cupón periódico:
- Construir la estructura de la anualidad (ak), recogiendo todas las características que le afecten.
- Normalizar la anualidad, obteniendo la anualidad normalizada (a’k) y el tanto normalizado (i’).
- Como la anualidad normalizada puede que no siga ningún tipo de ley, evitaremos trabajar con rentas y lo haremos con sumatorios y se planteará la equivalencia financiera entre el nominal del empréstito y los términos normalizados actualizados al tanto normalizado.
- Se sustituirá en el sumatorio la anualidad normalizada (a’k), por su valor.
- Lo que multiplique o divida a ak, al ser constante, se podrá extraer del sumatorio.
- Si hubiera algún término que se sumara o restara a ak (lotes), el sumatorio se descompondrá en dos sumatorios.
- Los sumatorios se convertirán en valores actuales de rentas (constantes o variables).
- Se despejará el primer término amortizativo (a1).
EJEMPLO 20
Se emite el siguiente empréstito:
- Títulos emitidos: 50.000.
- Nominal título: 1.000 euros.
- Duración: 9 años.
- Sorteos anuales, acumulándose a los sorteos un cupón del 10% anual.
- Premio de 50.000 euros a repartir entre los 100 primeros títulos amortizados cada año.
- Anualidades comerciales variables en progresión geométrica de razón 1,08.
Se pide:
- Anualidad del sexto año.
- Títulos amortizados en el cuarto año.
- Títulos en circulación a principios del quinto año.
Solución:
1. Estructura de la anualidad teórica
Anualidad variable en progresión geométrica de razón 1,08 destinada a amortizar los títulos reembolsándoles el nominal y el cupón acumulado en compuesta hasta el sorteo y pagar un lote constante.
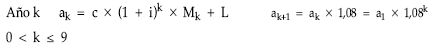
2. Normalización
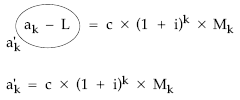
3. Planteamiento de la equivalencia entre el nominal del empréstito y las anualidades teóricas normalizadas trabajando con sumatorios
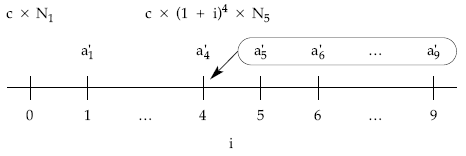
Gráficamente:
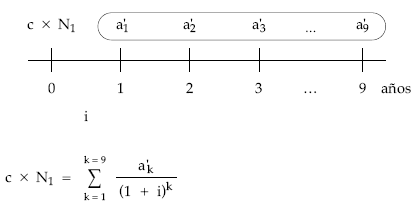
4. Sustitución de la anualidad normalizada por el valor obtenido en la normalización
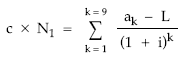
5. Separación del sumatorio en dos sumatorios parciales con igual denominador
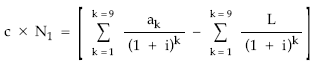
6. Conversión de los sumatorios en sus respectivos valores actuales de rentas
![]()
7. Sustitución en la expresión por valores numéricos y despeje de a1
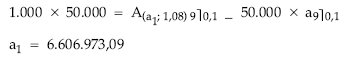
Anualidad del sexto año
a6 = a1 x 1,085 = 9.707.811,06
Títulos amortizados en el cuarto año
En la anualidad del año 4 todo se conoce salvo los títulos a amortizar, por tanto, sustituyendo en el término:
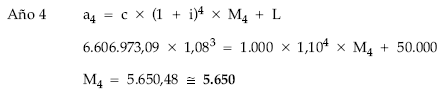
Títulos en circulación a principios del quinto año
Por el método prospectivo:
En 4: