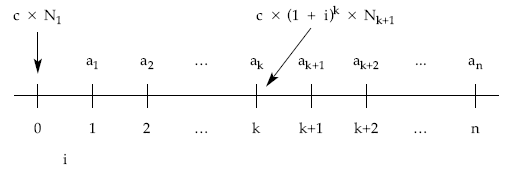
Este empréstito se caracteriza porque:
- Los términos amortizativos varían en progresión geométrica.
- La razón de la progresión permanece constante, durante toda la operación.
- El tanto del cupón permanece constante y se va acumulando en compuesta hasta el momento del sorteo.
La estructura de la anualidad de este empréstito puro es:
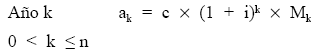
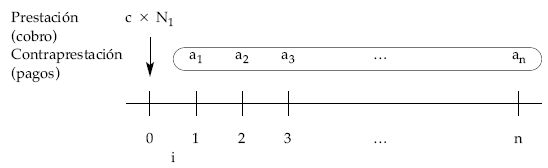
Gráficamente, el esquema de cobros y pagos que el empréstito origina para el emisor un empréstito de N1 títulos, de nominal c, que generan un interés i, a amortizar en n períodos con términos amortizativos variables en progresión geométrica de razón q conocida es el siguiente:
7.2.1. Pasos a seguir
7.2.1.1. Cálculo de los términos amortizativos (ak)
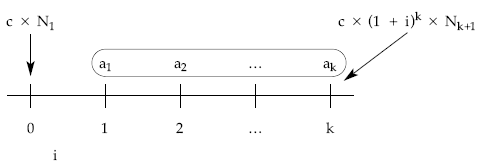
Se planteará una equivalencia financiera en el origen de la operación (momento 0) entre el importe nominal del empréstito y la renta en progresión geométrica formada por los términos amortizativos, cuyo valor actual se pondrá en función del primer término y la razón de la progresión.
Al desarrollar la equivalencia pueden darse dos casos según la relación entre la razón de la progresión que siguen los términos y el tipo de interés del cupón:
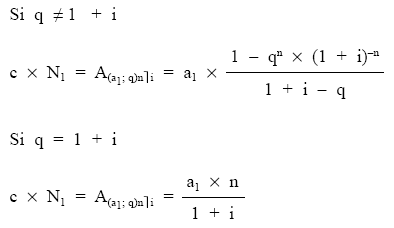
En ambos casos se despejará el primer término amortizativo (a1).
Una vez calculado el primer término amortizativo, el resto de términos se obtendrán a través de la ley de la progresión geométrica que siguen, así:
a2 = a1 x q
a3 = a2 x q = a1 x q2
…
ak+1 = ak x q = a1 x qk
…
an = an-1 x q = a1 x qn-1
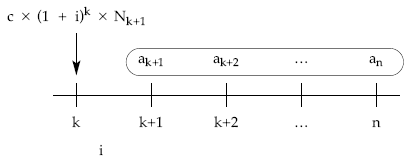
7.2.1.2. Cálculo de títulos amortizados: ley de recurrencia (Mk)
Para saber el número de títulos que en cada sorteo resultan amortizados podemos proceder de dos formas alternativas:
A) 1.ª posibilidad: dando valores a k en la estructura del término amortizativo
Conocida la cuantía del término a pagar el emisor en cada período (que previamente hemos calculado) y la que va a percibir cada título individualmente, se determinará fácilmente el número de títulos a amortizar. Así:
|
Período 1: |
a1 = c x (1 + i)1 x M1 | a1 –> M1 = ————— c x (1 + i) |
|
Período 2:
|
a2 = c x (1 + i)2 x M2 | a2 –> M2 = —————– c x (1 + i)2 |
| … |
B)
2.ª posibilidad: a través de la ley de recurrencia que siguen los títulos amortizados
La ley de recurrencia se obtendrá por relación, por cociente, de los términos amortizativos de dos períodos consecutivos cualesquiera, así:
|
Período k: |
ak = c x (1 + i)k x Mk |
| Período k+1: | ak+1 = c x (1 + i)k+1 x Mk+1 |
| ———————————– | |
|
ak c x (1 + i)k x Mk |
teniendo en cuenta que: ak+1 = ak x q
simplificando ambos miembros resulta:
1 Mk
—– = ——————–
q (1 + i) x Mk+1
de donde se obtiene:
q
Mk+1 = Mk x ———
1 + i
Expresión que permite conocer, a partir de los títulos amortizados en el sorteo anterior, los que corresponde amortizar en el presente.
7.2.1.3. Cálculo del total de títulos amortizados (mk)
Conocer la totalidad de títulos amortizados en un momento de tiempo concreto se puede hacer de dos formas posibles:
- Por diferencias, entre el número de títulos emitidos y los que aún están en circulación:
mk = N1 – Nk+1
- Por suma de los títulos amortizados hasta la fecha:
mk = M1 + M2 + … + Mk
7.2.1.4. Cálculo de títulos vivos a principio de cada período (Nk+1)
Podemos plantear este cálculo de varias formas:
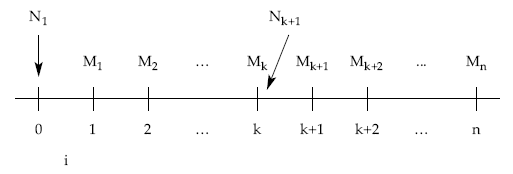
A) 1.ª posibilidad: a través de los títulos amortizados
- Método retrospectivo: considerando títulos ya amortizados.
Nk+1 = N1 – [M1 + M2 + … + Mk] = N1 – mk
- Método prospectivo: considerando los títulos pendientes de amortizar.
Nk+1 = Mk+1 + Mk+2 + … + Mn
B) 2.ª posibilidad: a través de términos amortizativos
Al trabajar con los términos amortizativos se deberán hacer de forma financiera (no bastará con sumar y restar aritméticamente, como en el caso anterior) puesto que los términos incorporan intereses y principal; habrá que mover financieramente las cantidades correspondientes.
• Método retrospectivo, a través de los términos amortizativos pasados.
en K se debe cumplir:
lo que se supondría la amortización anticipada en k = [lo recibido – lo pagado]k
![]()
de donde se despejaría el número de títulos en circulación en ese momento: Nk+1.
• Método prospectivo, a través de los términos amortizativos futuros.
en K se debe cumplir:
lo que se supondría la amortización anticipada en k = [cantidades pendientes de pagar]k
![]()
de donde se despejaría el número de títulos en circulación en ese momento: Nk+1.
EJEMPLO 19
Se emite el siguiente empréstito:
- Títulos emitidos: 10.000.
- Nominal del título: 1.000 euros.
- Duración: 5 años.
- No abono de cupones anuales, acumulándose a los sorteos, en régimen de compuesta, al 10% anual.
- Anualidades variables en progresión geométrica de razón 1,10.
Se pide:
Cuadro de amortización.
Solución:
Es un empréstito de cupón acumulado en compuesta que se les paga a los títulos amortizados en cada sorteo, siendo la anualidad pagada por el emisor variable en progresión geométrica de razón 1,10. La estructura del término amortizativo es:
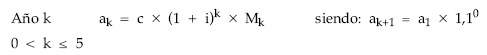
Gráficamente:
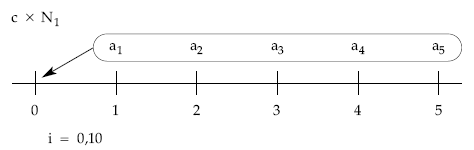
Planteando la equivalencia entre el nominal del empréstito y las anualidades pagadas, calcularemos la primera de ellas (a1):

y a partir de la primera, las demás se obtendrán a partir de la ley geométrica que siguen.
Cuadro de amortización
|
k
|
(1)
|
(2)
|
(3)
|
(4) = (2) x 1.000
x 1,10k |
(5) = (4)
|
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total tít. amort.
|
Amortización
|
Término amortizativo
|
|
1
2 3 4 5 |
10.000
8.000 6.000 4.000 2.000 |
2.000
2.000 2.000 2.000 2.000 |
2.000
4.000 6.000 8.000 10.000 |
2.200.000
2.420.000 2.662.000 2.928.200 3.221.020 |
2.200.000
2.420.000 2.662.000 2.928.200 3.221.020 |
(1) Cálculo de los títulos amortizados
Para conocer el número de títulos a amortizar en cada período, basta con darle valores a la anualidad, según el período que queramos calcular, siendo todo conocido salvo el Mk buscado:
|
Año 1: |
a1 = c x (1 + i)1 x M1 |
|
| 2.200.000 = 1.000 x 1,10 x M1 | M1 = 2.000 | |
|
Año 2: |
a2 = c x (1 + i)2 x M2 | |
| 2.420.000 = 1.000 x 1,102 x M2 | M2 = 2.000 | |
|
Año 3: |
a3 = c x (1 + i)3 x M3 | |
| 2.662.000 = 1.000 x 1,103 x M3 | M3 = 2.000 | |
|
Año 4: |
a4 = c x (1 + i)4 x M4 | |
| 2.928.000 = 1.000 x 1,104 x M4 | M4 = 2.000 | |
|
Año 5: |
a5 = c x (1 + i)5 x M5 | |
| 3.221.020 = 1.000 x 1,105 x M5 | M5 = 2.000 |
La razón de que haya resultado un empréstito con igual número de títulos amortizados en cada sorteo se debe a que la razón de la progresión que siguen las anualidades coincide con 1 + i (el tanto del cupón), de forma que el aumento del término coincide con el aumento del cupón acumulado, por lo que el número de títulos a amortizar permanece constante todos los sorteos.




