Este tipo de rentas se refiere a un conjunto de capitales cuyas cuantías van variando y lo hacen siguiendo una ley en progresión aritmética, esto es, cada término es el anterior aumentado (o disminuido) en una misma cuantía (que se denomina razón de la progresión aritmética) y que notaremos por d, siempre expresada en unidades monetarias.
Para calcular cualquier término basta con conocer, por tanto, el primero de ellos (c) y la razón de la progresión (d).
4.1.
RENTA VARIABLE EN PROGRESIÓN ARITMÉTICA, TEMPORAL, POSPAGABLE, INMEDIATA Y ENTERA
Vamos a estudiar una renta variable en progresión aritmética, temporal (tiene un número determinado de capitales), pospagable (los términos vencen al final del período), inmediata (valoraremos la renta en su origen y su final) y entera (términos y tanto están en la misma unidad de tiempo).
4.1.1. Cálculo del valor actual
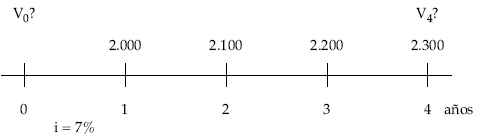
La representación gráfica de la renta anteriormente citada es la siguiente:
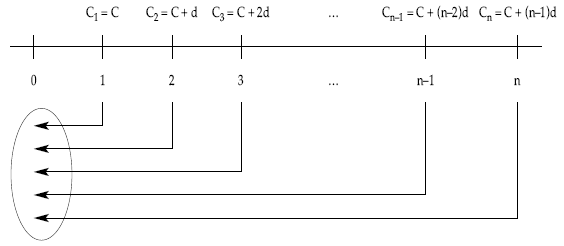
Aplicando la definición de valor actual y llevando los términos uno a uno, descontando en régimen de descuento compuesto al tanto de la renta i, desde donde están hasta el origen se obtiene el valor actual, que se nota con la siguiente terminología A(c; d) nùi, expresión que además de recoger la información de la renta, recoge la información de la progresión (c; d):
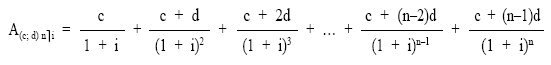
de donde finalmente se puede obtener la siguiente expresión:
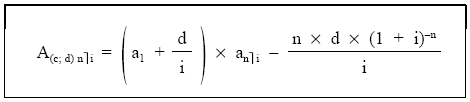
que se puede convertir en esta otra fórmula de cálculo:
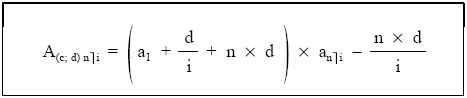
| Nota: se ha prescindido del desarrollo matemático de esta demostración, reflejando el resultado final del mismo. |
4.1.2. Cálculo del valor final
A partir del valor actual se podrá calcular cualquier otro valor financiero, utilizando la relación que existe entre los diferentes valores financieros en los distintos momentos de tiempo:
Valor final:
![]()
EJEMPLO 12
Hallar el valor actual y final de una corriente de gastos anuales vencidos de un negocio que el primer año van a ser 2.000 euros y se espera que aumenten 100 euros cada año, suponiendo una tasa de valoración del 7% y para un horizonte temporal de 4 años.
• Valor actual:
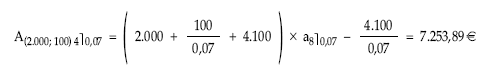
• Valor final:
![]()
| Nota: a idénticos resultados se hubiera llegado si valoramos uno a uno los capitales en la fecha de estudio. |
4.2. RENTAS PREPAGABLES
En este caso, basta con multiplicar por (1 + i) el valor actual o final (según proceda) de la renta pospagable.
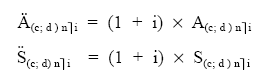
4.3. RENTAS PERPETUAS
El cálculo de la renta en progresión geométrica perpetua se realiza, como para cualquier renta perpetua, a través del límite cuando la duración (n) tiende a infinito:
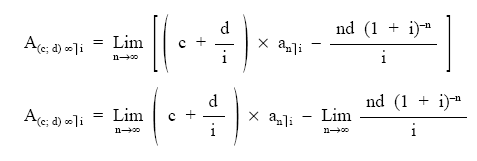
resultando finalmente:
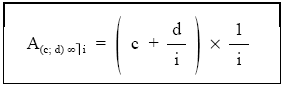
Todas las fórmulas se han desarrollado suponiendo que la razón es positiva (d > 0), es decir, que los términos van aumentando, aunque siguen siendo válidas para el caso contrario, bastaría con cambiar el signo de la razón (d) en las fórmulas.
4.4. RENTAS DIFERIDAS Y ANTICIPADAS
Serán diferidas cuando se valoran con anterioridad a su origen y anticipadas cuando se valoran después de su final.
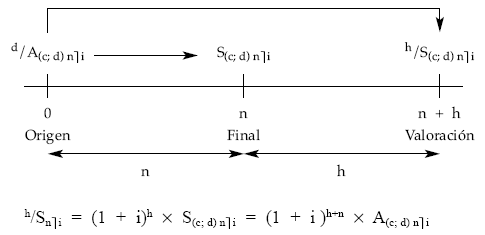
Como en cualquier otro tipo de renta, se pueden establecer relaciones entre diferentes valores de la renta. Así:
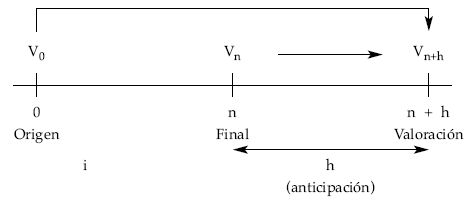
Vn Vn+h
V0 = ———— = ————–
(1 + i)n (1 + i)n+h




