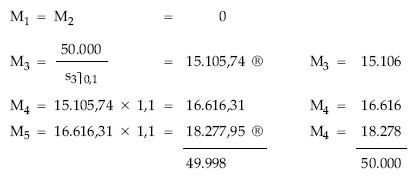Empréstitos diferidos (con diferimiento) son aquellos en los que se retrasa la realización del primer sorteo de títulos, el cual ya no tendrá lugar al finalizar el primer período de vida de la operación.
Así pues, durante una primera etapa no se realizan sorteos y amortización de títulos y, por tanto, el emisor no paga valores de reembolso ni nada que tenga que ver con los sorteos (lotes, amortización seca, …); sí que se pagarán los cupones y, si procede, gastos de administración.
Por tanto, a la hora de determinar la estructura de la(s) anualidad(es) habrá una diferente para el período durante el cual no hay sorteos (período de diferimiento) y al menos otra, diferente para el resto de períodos del empréstito.
El cálculo del término amortizativo durante el período de diferimiento es fácil de obtener a partir de datos de partida, pues recoge el cupón periódico que perciben todos los títulos emitidos (N1) y, si tiene, gastos de administración. Para obtener la otra anualidad habrá que proceder como si el empréstito comenzara al final del período de diferimiento, planteando en ese punto la equivalencia entre el nominal del empréstito en ese punto y la actualización de las restantes anualidades (normalizadas, si tiene características comerciales).
El diferimiento es posible cualesquiera que sean las características que presente el empréstito y también con independencia de que la anualidad del mismo sea constante o variable. En este sentido, a la hora de realizar los cálculos se aplicarán las expresiones que procedan según el tipo de empréstito.
EJEMPLO 11
Se emite el siguiente empréstito:
- Títulos emitidos: 50.000.
- Nominal del título: 1.000 euros.
- Cupón anual: 110 euros.
- Duración: 5 años.
- Los títulos se adquieren al 90%.
- Sorteos anuales, amortizándose los títulos con prima de 100 euros, teniendo lugar el primer sorteo al tercer año de la emisión.
- Gastos iniciales de 500.000 euros a cargo de emisor.
- Gastos de administración del 2‰ sobre las cantidades pagadas anualmente a los obligacionistas.
Se pide:
- Anualidades del empréstito.
- Cuadro de amortización.
Solución:
Cálculo de las anualidades
Hay un diferimiento de dos años, durante los cuales el emisor solamente pagará un cupón constante (c x i) a los títulos emitidos así como los gastos de administración calculados sobre dichos intereses. Durante los tres últimos años, la anualidad se destina a pagar el mismo cupón a los títulos en circulación (cada vez menores), amortizar con prima constante los títulos que corresponda y pagar los gastos de administración. Las estructuras de los términos amortizativos serán:
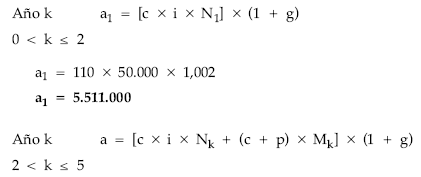
a
——– = c x i x Nk + (c + p) x Mk
1 + g
a i
——————– = c x ——– x Nk + Mk
(1 + g) x (c + p) c + p
a x c c x i
———————- = c x ——— x Nk + c x Mk
(1 + g) x (c + p) c + p
siendo:
a x c i x c 110
a' = ———————- i' = ——- = —————– = 0,10
(1 + g) x (c + p) c + p 1.000 + 100
queda:
a' = c x i' x Nk + c x Mk
planteando la equivalencia en 2:
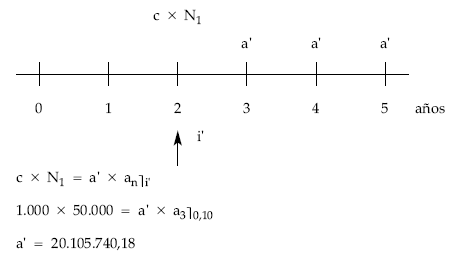
teniendo en cuenta que:
a x c
a' = ———————
(1 + g) x (c + p)
y sustituyendo los datos conocidos, se despeja a:
a
20.105.740,18 = ————————————-
(1 + 0,002) x (1.000 + 100)
a = 22.160.547,82
Cuadro de amortización (3 líneas)
|
(1)
|
(2)
|
(3) = (1) x 110
|
(4) = (2) x 1.100
|
(5) = 2‰ [(3) + (4)]
|
(6) = (3) + (4) + (5)
|
|
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Intereses
|
Amortización
|
Gastos admón.
|
Término amortizativo
|
|
1
2 3 4 5 |
50.000
50.000 50.000 34.894 18.278 |
–
– 15.106 16.616 18.278 |
5.500.000
5.500.000 5.500.000 3.838.340 2.010.580 |
–
– 16.616.600 18.277.600 20.105.800 |
11.000,0
11.000,0 44.233,2 44.231,9 44.232,8 |
5.511.000,0
5.511.000,0 22.160.833,2 22.160.171,9 22.160.612,8 |
Cálculo de los títulos amortizados