En este tipo de empréstito, el emisor se compromete a amortizar todos los períodos el mismo número de títulos, por tanto, la cantidad destinada al reembolso se mantiene constante durante toda la operación.
3.1.1. Pasos a seguir
Para el caso de un empréstito de N1 títulos, de nominal c, cupón periódico c x i, con una duración de n períodos se calculará en primer lugar todo lo que tenga que ver con la amortización de títulos, fáciles de obtener, y a continuación lo referente a los cupones y, finalmente, los términos amortizativos.
3.1.1.1. Cálculo del número de títulos amortizados en cada sorteo (M)
Sabiendo que la suma de los títulos amortizados en cada sorteo es el número de títulos emitidos, se debe cumplir:
N1 = M1 + M2 + M3 + … + Mn = M x n
de donde se obtiene:
N1
M = ——
n
Donde n representa el número de sorteos realizados a lo largo de la vida del empréstito.
3.1.1.2. Cálculo del total de títulos amortizados después de k períodos (mk)
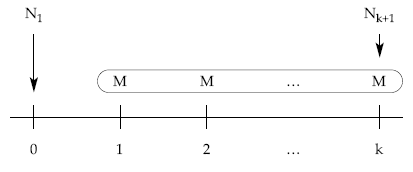
Conocidos los títulos que se amortizan en cada sorteo, el total de ellos retirados de la circulación hasta una fecha concreta vendrá dado por la suma aritmética de los títulos amortizados correspondiente a los períodos transcurridos.
mk = M1 + M2 + … + Mk = M x k
3.1.1.3. Cálculo de los títulos en circulación a principios del período k+1 (Nk+1)
Se realizará a través de los títulos amortizados (pasados o futuros).
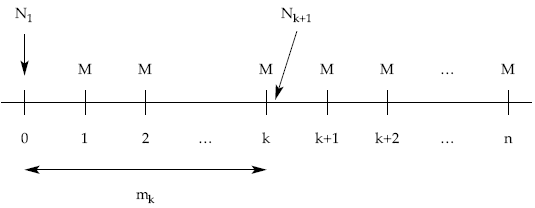
- Método retrospectivo: los títulos pendientes de amortizar serán los emitidos minorados en los ya amortizados hasta ese momento.
Nk+1 = N1 – mk = N1 – M x k
- Método prospectivo: los títulos en circulación serán la suma aritmética de los que aún quedan pendientes de ser amortizados.
Nk+1 = (n – k) x M
3.1.1.4. Cálculo del pago de cupones en el período k + 1
Los intereses de cualquier período se calcularán a partir de los títulos en circulación a principios de ese período, a los que se les entregará el cupón acordado (c x i).
Período k+1: c x i x Nk+1
3.1.1.5. Cálculo de los términos amortizativos: ley de recurrencia (ak)
Al mantenerse constante la parte del término amortizativo que se destina al reembolso de títulos e ir disminuyendo la cantidad destinada a pago de cupones (porque va siendo cada vez menor el número de títulos en circulación que tiene derecho a cobrarlo), los términos amortizativos necesariamente tendrán que ir decreciendo. Además, los términos variarán como lo hacen las cantidades destinadas al pago de cupones y seguirán una ley matemática.
La estructura del término amortizativo quedará de la siguiente forma:
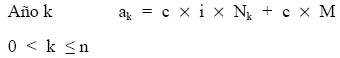
El cálculo de los diferentes términos se podrá realizar de dos formas posibles:
A) 1.ª posibilidad: dando valores a k en la estructura del término amortizativo
Calculando el importe del pago de cupones a realizar a los títulos aún en circulación y añadiendo el valor de reembolso constante ya conocido:
Período 1: a1 = c x i x N1 + c x M
Período 2: a2 = c x i x N2 + c x M = c x i x (N1 – M) + c x M
…
B)
2.ª posibilidad: a través de la ley de recurrencia que siguen los términos amortizativos
Se calcula el primer término y el resto se obtiene a través de la ley de recurrencia que siguen y que se obtendrá al relacionar, por diferencias, dos términos amortizativos consecutivos cualesquiera:
Período k: ak = c x i x Nk + c x M
Período k+1: ak+1 = c x i x Nk+1 + c x M
—————————————————————
ak – ak+1 = c x i x Nk – c x i x Nk+1 + c x M – c x M
simplificando: ak – ak+1 = c x i x (Nk – Nk+1)
siendo :
Nk – Nk+1 = M
se puede deducir:
ak+1 = ak – c x i x M
lo que indica que cualquier término amortizativo es el anterior menos una cuantía constante, es decir, los términos varían en progresión aritmética de razón – (c x i x M), por lo que todos los términos se pueden calcular a partir del primero de ellos, en base a esa recurrencia:
ak+1 = a1 – k x c x i x M
Si hay características comerciales, éstas sólo afectarían al cálculo de los términos amortizativos y, en consecuencia, a la ley de recurrencia que siguen. No se normaliza.
EJEMPLO 6
Construir la fila octava del cuadro de amortización del siguiente empréstito:
- Títulos emitidos: 100.000.
- Nominal del título: 1.000 euros.
- Duración: 10 años.
- Los títulos se adquieren al 90%.
- Cupón anual: 120 euros.
- Sorteos anuales, amortizándose el mismo número de títulos, con prima de 100 euros por título.
- Premio de 5.000 euros para cada uno de los 100 primeros títulos amortizados cada año.
- Gastos de administración del 1‰ sobre los cupones pagados anualmente.
Solución:
Es un empréstito de cupón periódico constante, amortización con prima de reembolso, lote constante (5.000 x 100), gastos de administración calculados exclusivamente sobre el pago de cupones a los obligacionistas y siendo el número de títulos amortizados constantes. La estructura de la anualidad será:
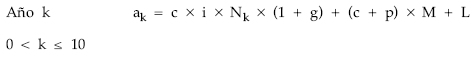
|
|
(2)
|
(1)
|
(3) = 120 x (2)
|
(4) = 1.100 x (1)
|
(5) = 5.000 x 100
|
(6) = 1‰ x (3)
|
(7) = (3)
+ (4) + (5) + (6) |
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Intereses
|
Amortiz.
|
Lotes
|
Gastos admón.
|
Término
amortizativo |
|
8
|
30.000
|
10.000
|
3.600.000
|
11.000.000
|
500.000
|
3.600
|
15.103.600
|
100.000
(1) M1 = M2 = … = M10 = M = ———— = 10.000
10
(2) N8 = N1 – m7 = 3 x M = 30.000
La prima de emisión de 100 euros por título no afecta a los términos amortizativos.




