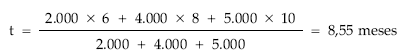La sustitución de un(os) capital(es) por otro u otros de vencimientos y/o cuantías diferentes a las anteriores, sólo se podrá llevar a cabo si financieramente resultan ambas alternativas equivalentes.
Para ver si dos alternativas son financieramente equivalentes se tendrán que valorar en un mismo momento de tiempo y obligar a que tengan las mismas cuantías. A este momento de tiempo donde se realiza la valoración se le denomina época o fecha focal o, simplemente, fecha de estudio.
Para plantear una sustitución de capitales el acreedor y el deudor han de estar de acuerdo en las siguientes condiciones fundamentales:
- Momento de tiempo a partir del cual se computan los vencimientos.
- Momento en el cual se realiza la equivalencia, teniendo en cuenta que al variar este dato varía el resultado del problema.
- Tanto de valoración de la operación.
- Decidir si se utiliza la capitalización o el descuento.
Casos posibles:
- Determinación del capital común.
- Determinación del vencimiento común.
- Determinación del vencimiento medio.
2.2.1. Determinación del capital común
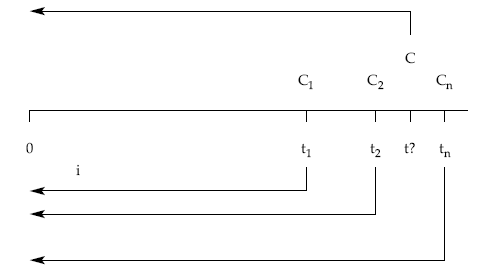
Es la cuantía C de un capital único que vence en el momento t, conocido, y que sustituye a varios capitales C1, C2, …, Cn, con vencimientos en t1, t2, … , tn, respectivamente, todos ellos conocidos en cuantías y tiempos.
Para su cálculo se valorarán en un mismo momento al tanto elegido, por una parte, los capitales de los que se parte y, por otra, el capital único desconocido que los va a sustituir.
Si la equivalencia se plantea en 0:
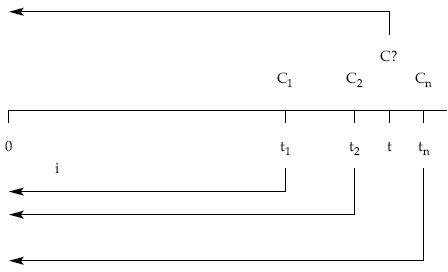
Realizando la valoración con tipo de interés (i):
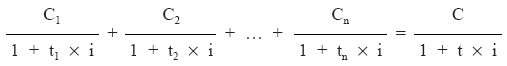
de donde se despejará C.
Realizando la valoración a tipo de descuento (d):
C1 x (1 – t1 x d) + C2 x (1 – t2 x d) + … + Cn x (1 – tn x d) = C x (1 – t x d)
despejando finalmente C, queda:
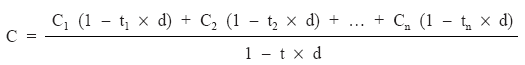
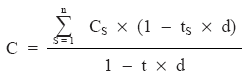
Si el estudio se realiza en el momento t, habrá que tener en cuenta que aquellos capitales que tengan un vencimiento inferior a t habrá que capitalizarlos (empleando un tipo de interés i), mientras que aquellos capitales con vencimientos superiores habrá que descontarlos, pudiéndose emplear bien un tipo de interés o bien de descuento.
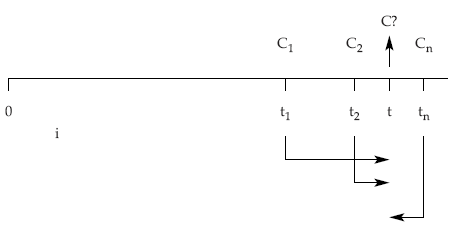
Realizando la valoración con tipo de interés (i):
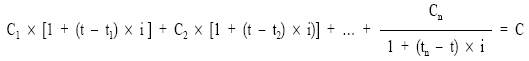
Se despejará C, pues todo lo demás se conoce.
EJEMPLO 11
Un señor tiene tres deudas de 2.000, 4.000 y 5.000 euros con vencimientos a los 6, 8 y 10 meses, respectivamente.
Propone sustituir las tres deudas por una sola a pagar a los 9 meses.
Se pide:
Calcular el importe a pagar si la operación se concierta al 8% de interés simple anual.
1.er caso: fecha de estudio en 0:
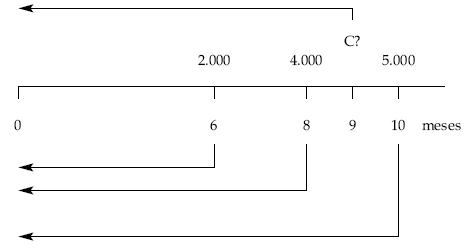
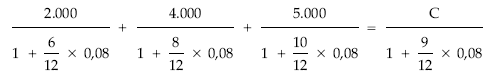
C = 11.032,53 €
2.º caso: fecha de estudio en 9:
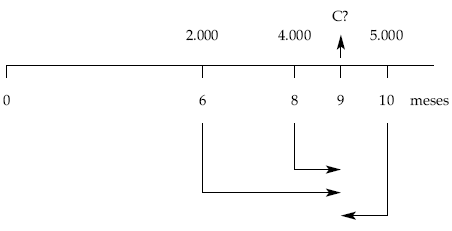
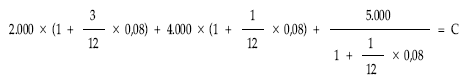
C = 11.033,56 €
2.2.2. Determinación del vencimiento común
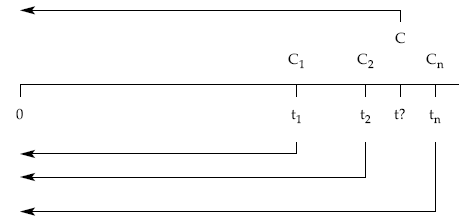
Es el momento de tiempo t en que vence un capital único C, conocido, que sustituye a varios capitales C1, C2, … , Cn, con vencimientos en t1, t2, … , tn, respectivamente, todos ellos conocidos.
Se tiene que cumplir:
![]()
Para obtener este vencimiento habría que proceder de la misma forma que en el caso del capital común, siendo ahora la incógnita el momento donde se sitúa ese capital único. Así, por ejemplo, si la equivalencia se realiza en el origen a tanto de interés (i):
Realizando la valoración con tipo de interés (i):
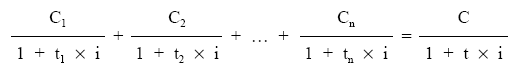
simplificando:
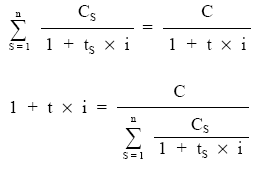
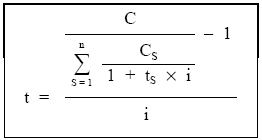
Realizando la valoración a tipo de descuento (d):
C1 x (1 – t1 x d) + C2 x (1 – t2 x d) + … + Cn x (1 – tn x d) = C x (1 – t x d)
se quitan los paréntesis y queda:
C1 – C1 x t1 x d + C2 – C2 x t2 x d + … + Cn – Cn x tn x d = C – C x t x d
reordenando en el primer miembro:
C1 + C2 + … + Cn – d [C1 x t1 + C2 x t2 + … + Cn x tn] = C – C x t x d
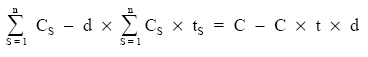
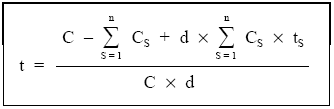
de donde se despeja t.
EJEMPLO 12
Un señor tiene tres deudas de 2.000, 4.000 y 5.000 euros con vencimientos a los 6, 8 y 10 meses, respectivamente.
De acuerdo con el acreedor acuerdan hoy sustituir las tres deudas por una sola de 11.200 euros.
Se pide:
Calcular el momento de pago si la operación se concierta al 8% de interés simple anual. La fecha de estudio es el momento cero.
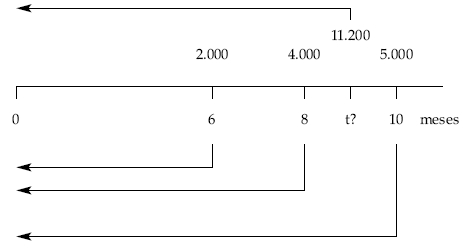
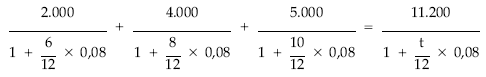
t = 11,41 meses
2.2.3. Determinación del vencimiento medio
Es el momento de tiempo t en que vence un capital único C, conocido, que sustituye a varios capitales C1, C2, … , Cn, con vencimientos en t1, t2, … , tn, respectivamente, todos ellos conocidos.
Se tiene que cumplir:
C = C1+ C2 +… + Cn
El cálculo es idéntico al vencimiento común, lo único que varía es la cuantía del capital único que sustituye al conjunto de capitales de los que se parte, que ahora debe ser igual a la suma aritmética de las cuantías a las que sustituye.
Realizando el estudio de equivalencia en el origen y empleando un tipo de descuento d, quedaría así:
C1 x (1 – t1 x d) + C2 x (1 – t2 x d) + … + Cn x (1 – tn x d) = C x (1 – t x d)
quitando los paréntesis:
C1 – C1 x t1 x d + C2 – C2 x t2 x d + … + Cn – Cn x tn x d = C – C x t x d
reordenando en el primer miembro:
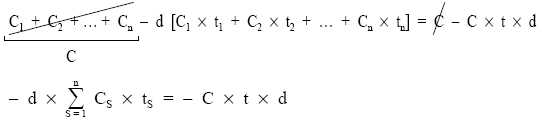
dividiendo la ecuación por – d:
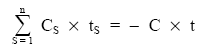
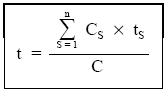
En definitiva, el vencimiento medio resulta ser una media aritmética ponderada de los vencimientos de los capitales de partida, siendo el importe de dichos capitales los factores de ponderación.
EJEMPLO 13
Un señor tiene tres deudas de 2.000, 4.000 y 5.000 euros con vencimientos a los 6, 8 y 10 meses, respectivamente.
De acuerdo con el acreedor acuerdan hoy sustituir las tres deudas por una sola de 11.000 euros.
Se pide:
Calcular el momento de pago si la operación se concierta al 8% de descuento simple anual. La fecha de estudio es el momento cero.
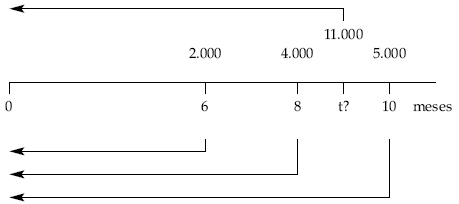
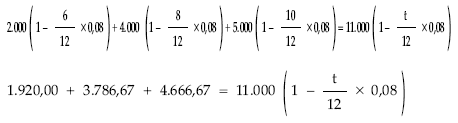
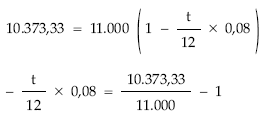
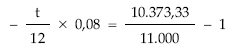
t = 8,55 meses
De otra forma: