Se trata de ver los cálculos a realizar con el fin de construir el cuadro de amortización del empréstito, esto es, saber la cantidad a pagar en cada momento (término amortizativo) y su descomposición en cuota de amortización (c x Mk) y cuota de interés (c x i x Nk).
2.1.1. Cálculo del término amortizativo (a)
Los pagos constantes que se realizan durante la vida del empréstito incorporan, en parte el coste del aplazamiento (pago de cupones), en parte la devolución de una porción de la deuda (amortización de títulos). Para calcular el término amortizativo bastaría con plantear una equivalencia financiera en el momento 0 entre el nominal del empréstito y la renta formada por los términos amortizativos:
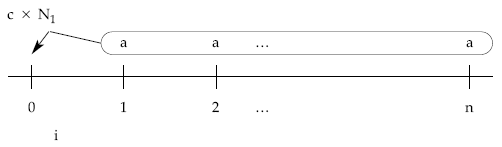
resultando:
![]()
de donde se despeja el término a:
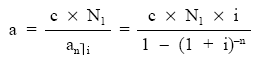
Es lo que se denomina el término amortizativo teórico (a diferencia de los que aparecen en el cuadro que se les conoce como términos amortizativos prácticos o reales).
2.1.2. Cálculo de títulos amortizados: ley de recurrencia (Mk)
Dada la estructura del término amortizativo (a) constante e ir disminuyendo la parte del mismo destinada al pago de cupones (porque va siendo cada vez menor el número de títulos en circulación que tienen derecho a cobrarlo), el valor destinado a reembolsar títulos necesariamente tendrá que ir creciendo y, por tanto, el número de títulos amortizados en cada sorteo.
Se plantea la necesidad de saber cómo se obtiene el número de títulos que en cada sorteo resultan amortizados. Para ello podemos proceder de dos formas alternativas:
2.1.2.1.
1.ª posibilidad: dando valores a k en la estructura del término amortizativo
Conocida la cuantía del término a pagar en cada período y la cantidad destinada al pago de cupones, se puede saber cuánto se destina a amortizar y, por tanto, cuántos títulos se amortizarán en cada momento. Así:
Período 1: a = c x i x N1 + c x M1 –> c x M1 = a – c x i x N1
a – c x i x N1
M1 = ——————-
c
Período 2: a = c x i x N2 + c x M2 –> c x M2 = a – c x i x (N1 – M1)
a – c x i x (N1 – M1)
M2 = —————————-
c
Siguiendo de la misma manera para el resto de períodos completaríamos el cálculo de títulos amortizados en cada sorteo. A pesar de la simplicidad del cálculo, resulta poco práctico, sobre todo cuando el número de sorteos es elevado. Conviene, pues, buscar un procedimiento que permita establecer, si es posible, alguna relación (ley de recurrencia) a la hora de calcular los Mk.
2.1.2.2.
2.ª posibilidad: a través de la ley de recurrencia que siguen los títulos amortizados
Como antes se ha comentado, al ser constante el término amortizativo y las cantidades destinadas al pago de cupones decrecientes, las cuantías destinadas a amortización necesariamente tendrán que ir creciendo. Además, varían siguiendo una ley matemática (ley de recurrencia).
La ley de recurrencia es la relación que existe entre dos términos consecutivos, en este caso, las cantidades destinadas a amortizar títulos. Para buscarla se relacionan por diferencias los términos amortizativos de dos períodos consecutivos cualesquiera, así:
Período k: a = c x i x Nk + c x Mk
Período k+1: a = c x i x Nk+1 + c x Mk+1
———————————————————
a – a = c x i x (Nk – Nk+1) + c x Mk – c x Mk+1
Siendo: Nk – Nk+1 = Mk
0 = c x i x Mk + c x Mk – c x Mk+1
dividiendo toda la expresión por c:
0 = i x Mk + Mk – Mk+1
de donde se obtiene:
Mk+1 = Mk x (1 + i)
Al aplicar esta ley para cualesquiera dos períodos consecutivos, se observa que varían siguiendo una progresión geométrica de razón 1 + i, por tanto, cualquier Mk se puede calcular a partir del anterior, del primero o de cualquiera conocido. Con carácter genérico, se pondrán en función del primero –que es el más fácil de obtener–:
Mk+1 = M1 x (1 + i)k
2.1.3. Cálculo de títulos amortizados en el primer sorteo (M1)
Una vez calculado M1, todos los demás se podrán obtener aplicando la ley de recurrencia anterior. El cálculo del número de títulos amortizados en el primer sorteo se puede realizar de dos formas posibles:
2.1.3.1.
1.ª posibilidad: a través de la estructura del primer término amortizativo
Período 1: a = c x i x N1 + c x M1
a – c x i x N1
donde es conocido todo salvo M1 –> M1 = ——————-
c
lo que implica haber calculado previamente el término amortizativo (a).
2.1.3.2. 2.ª posibilidad: a través de los títulos emitidos
En todo empréstito se cumple que la suma aritmética de los títulos amortizados en cada período coincide con el número de títulos inicialmente emitidos:
M1 + M2 + M3 + … + Mn = N1
Además, en este tipo de empréstito todos los títulos amortizados se pueden poner en función del primero de ellos por la ley de recurrencia antes calculada, por lo que la igualdad anterior quedará de la siguiente forma:
M1 + M1 x (1 + i) + M1 x (1 + i)2 + … + M1 x (1 + i)n-1 = N1
Simplificando la expresión:
M1 x [1 + (1 + i) + (1 + i)2 + … + (1 + i)n-1] = N1
donde el corchete es el valor final de una renta unitaria, pospagable e inmediata de n términos, por tanto:
![]()
de donde:
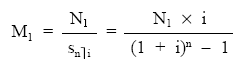
2.1.4. Cálculo del total de títulos amortizados (mk)
Los títulos amortizados en un momento de tiempo concreto se pueden obtener de dos formas posibles:
• Por diferencias, entre el número de títulos emitidos y los que aún están en circulación:
mk = N1 – Nk+1
• Por suma de los títulos amortizados hasta la fecha:
mk = M1 + M2 + … + Mk
Además, todos los títulos amortizados se pueden poner en función del primero de ellos, según la ley de recurrencia que siguen:
mk = M1 + M1 x (1 + i) + M1 x (1 + i)2 + … + M1 x (1 + i)k-1
Simplificando la expresión:
mk = M1 x [1 + (1 + i) + (1 + i)2 + … + (1 + i)k-1]
donde el corchete es el valor final de una renta unitaria, pospagable e inmediata de k términos, por tanto:
![]()
2.1.5. Cálculo de títulos vivos a principios de cada período (Nk+1)
Podemos plantear este cálculo de varias formas:
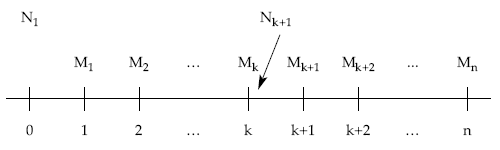
2.1.5.1. 1.ª posibilidad: a través de los títulos amortizados
- Método retrospectivo: considerando títulos ya amortizados:
![]()
- Método prospectivo: considerando los títulos pendientes de amortizar:
![]()
2.1.5.2. 2.ª posibilidad: a través de términos amortizativos
Al trabajar con los términos amortizativos se deberán hacer de forma financiera (no bastará con sumar y restar aritméticamente, como en el caso anterior) puesto que los términos incorporan intereses y principal; habrá que mover financieramente las cantidades correspondientes.
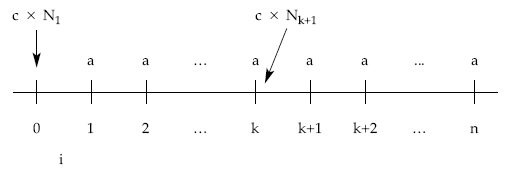
• Método retrospectivo, a través de los términos amortizativos pasados.
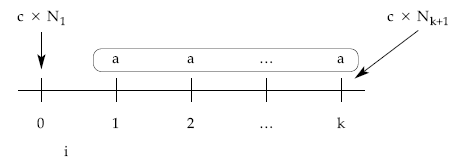
Se ha de cumplir la equivalencia en el momento elegido (k) entre lo que le supone al emisor amortizar de una sola vez los títulos aún en circulación (amortización anticipada) y lo que aún debe (la diferencia entre lo que el emisor recibió en la emisión y lo que hasta la fecha ya ha pagado):
en k:
Lo que se supondría la amortización anticipada en k = [lo recibido – lo pagado]k
es decir:
![]()
de donde se despejaría el número de títulos en circulación en ese momento: Nk+1.
- Método prospectivo, a través de los términos amortizativos futuros.
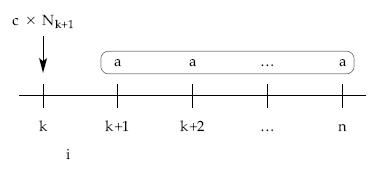
Se ha de cumplir la equivalencia en el momento elegido entre lo que supone amortizar de una sola vez los títulos aún en circulación (amortización anticipada) y lo que debería seguir pagando el emisor en caso de continuar con el empréstito hasta el final.
en k:
Lo que se supondría la amortización anticipada en k = [cantidades pendientes de pagar]k
es decir:
![]()
de donde se despejaría el número de títulos en circulación en ese momento: Nk+1.
2.1.6. Cálculo del importe a pagar de cupones en el período k+1
Los intereses de cualquier período se calcularán a partir de los títulos en circulación a principios de ese período, a los que se les entregará el cupón acordado (c x i).
Período k + 1: c x i x Nk+1
EJEMPLO 2
Se emite el siguiente empréstito:
- Títulos emitidos: 100.000.
- Nominal título: 1.000 euros.
- Cupón anual (c x i): 120 euros.
- Duración: 5 años.
- Sorteos anuales, amortizándose los títulos por el nominal.
- Anualidad constante.
Se pide:
- Anualidad del empréstito.
- Cuadro de amortización.
Solución:
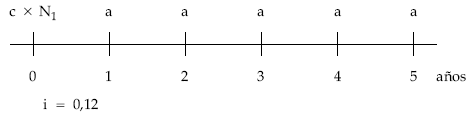
Cálculo de la anualidad:
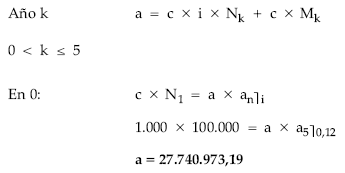
Cálculo de los títulos amortizados:

Para calcular el número definitivo de títulos amortizados en cada sorteo, seguiremos el denominado «método del redondeo», que consiste en calcular en primer lugar los títulos que teóricamente corresponde amortizar en cada sorteo (con decimales). A continuación se suman solamente las partes enteras (99.996) y los títulos que faltan hasta completar los que se emitieron (4 en nuestro caso), se reparten teniendo preferencia los sorteos con mayor decimal y correspondiendo como máximo un título por sorteo.
Cuadro de amortización:
|
|
(1)
|
(2)
|
(3)
|
(4) = (1) x 120
|
(5) = (2) x 1.000
|
(6) = (4) + (5)
|
|
Año
|
Títulos vivos
|
Títulos amortiz.
|
Total
tít. amort. |
Intereses
|
Amortización
|
Término amortizativo
|
|
1
2 3 4 5 |
100.000
84.259 66.629 46.884 24.769 |
15.741
17.630 19.745 22.115 24.769 |
15.741
33.371 53.116 75.231 100.000 |
12.000.000
10.111.080 7.995.480 5.626.080 2.972.280 |
15.741.000
17.630.000 19.745.000 22.115.000 24.769.000 |
27.741.000
27.741.080 27.740.480 27.741.080 27.741.280 |
La columna (1) recoge los títulos en circulación a principios de cada período, que serán los que tengan derecho a percibir el cupón al final del período (4). La columna (2) recoge los títulos que resultan amortizados al final de cada período y que serán los que reciban el valor de reembolso (5). El pago finalmente efectuado por el emisor en cada momento será eltérmino amortizativo (6).
La cuantía de los términos amortizativos (también denominada anualidad práctica) no coincide con el importe calculado anteriormente (27.740.973,19). Esto se debe al redondeo efectuado en los títulos que resultan amortizados en cada sorteo.




