Considerando que el importe del préstamo es C0, con un tipo de interés anticipado i*, y amortizable en n períodos, en este caso debe cumplirse que: A1 = A2 = A3 = = … = An = A
11.2.1. Pasos a seguir
En este caso, al igual que ocurría cuando se vio el préstamo lineal con intereses vencidos, se calcula en primer lugar todo lo que tenga que ver con las cuotas de amortización, fáciles de obtener, a continuación los intereses y, finalmente, los términos amortizativos.
11.2.1.1. Cálculo de la cuota de amortización (A)
Sabiendo que la suma de todas las cuotas de principal es el importe del préstamo y que, además, éstas se mantienen constantes se debe cumplir:
C0 = A1 + A2 + A3 + … + An = A x n
de donde se obtiene:
C0
A = ——–
n
11.2.1.2. Cálculo del total amortizado después de k períodos (mk)
mk = A1 + A2 + … + Ak = A x k
11.2.1.3. Cálculo del capital vivo a principios del período k+1 (Ck)
El carácter prepagable de los intereses no afecta a las cuotas de amortización que sigue siendo pospagable.
A) 1.ª posibilidad: por el método retrospectivo
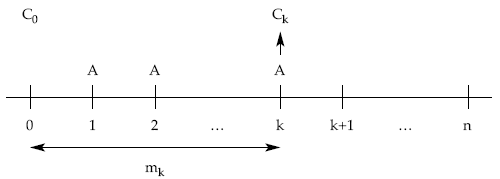
El capital pendiente será el importe del préstamo disminuido en la totalidad de las cuotas de amortización ya practicadas.
Ck = C0 – mk = C0 – [A + A + … + A] = C0 – A x k
B) 2.ª posibilidad: por el método prospectivo
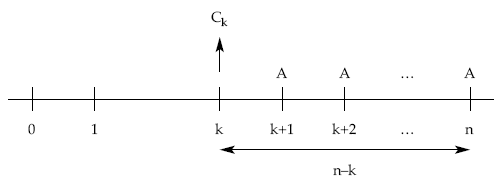
El capital pendiente será la suma aritmética de las cuotas de amortización aún pendientes de realizar.
Ck = Ak+1 + Ak+2 + … + An = (n – k) x A
11.2.1.4. Cálculo de cuota de interés de período k + 1 (Ik+1)
Los intereses de cualquier período se calcularán a partir de la deuda pendiente a principios de ese período, al tanto efectivo vigente durante el mismo, pero se pagan al principio de dicho período, así en el momento k (principios de k + 1) se pagan los intereses del período k + 1.

En k:
Ik+1 = Ck x i*
11.2.1.5. Cálculo de los términos amortizativos: ley de recurrencia (ak)
Puesto que los términos amortizativos son la suma de la cuota de interés (decrecientes porque se calculan sobre capitales cada vez menores) y la cuota de amortización (en este caso constantes), los términos variarán como lo hacen las cuotas de interés y seguirán una ley matemática.
1.ª posibilidad: calcular el importe del término amortizativo a través de su propia estructura, calculando la cuota de interés y añadiendo la cuota de amortización constante ya conocida:
En 0: a0 = I1 = C0 x i*
En 1: a1 = I2 + A = C1 x i* + A
En 2: a2 = I3 + A = C2 x i* + A = (C1 – A) x i* + A
…
2.ª posibilidad: consistirá en calcular el primer término y obtener todos a través de la ley de recurrencia que éstos siguen y que se obtiene al relacionar, por diferencias, dos términos amortizativos consecutivos cualesquiera:´

En k: ak = Ik+1 + A = Ck x i* + A
En k+1: ak+1 = Ik+2 + A = Ck+1 x i* + A
——————————————-
ak – ak+1 = (Ck – Ck+1) x i* + A – A
siendo: Ck – Ck+1 = A
resulta:
ak – ak+1 = A x i*
De donde se obtiene: ak+1 = ak – A x i*, lo que indica que cualquier término amortizativo es el anterior menos una cuantía constante, es decir, los términos varían en progresión aritmética de razón – (A x i*).




