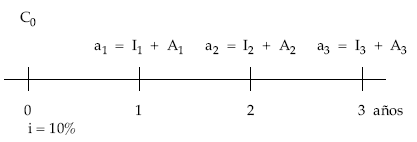El préstamo es una operación financiera de prestación única y contraprestación múltiple. En ella, una parte (llamada prestamista) entrega una cantidad de dinero (C₀) a otra (llamada prestatario) que lo recibe y se compromete a devolver el capital prestado en el (los) vencimiento(s) pactado(s) y a pagar unos intereses (precio por el uso del capital prestado) en los vencimientos señalados en el contrato.

La operación de amortización consiste en distribuir con periodicidad la devolución del principal (C₀), junto con los intereses que se vayan devengando a lo largo de la vida del préstamo. Los pagos periódicos que realiza el prestatario tienen, pues, la finalidad de reembolsar, extinguir o amortizar el capital inicial. Esto justifica el nombre de operación de amortización y el de términos amortizativos que suele asignarse a estos pagos.

1.1. PRINCIPALES SISTEMAS DE AMORTIZACIÓN DE PRÉSTAMOS

Según la finalidad a la que se destinen los términos amortizativos es posible admitir diversas interpretaciones de amortización, es decir, diferentes formas de llevar a cabo la amortización (devolución) del capital inicial: es lo que se denomina «sistema amortizativo» o «sistema de amortización» del préstamo.

a) Préstamos amortizables mediante reembolso único del principal al final de la operación.

• Sin pago periódico de intereses: préstamo simple.
• Con pago periódico de intereses: sistema americano.

b) Préstamos reembolsables mediante una serie de pagos periódicos que constituyan renta, esto es, fraccionamiento del principal en varios pagos parciales (cuotas de amortización) con vencimientos periódicos, que se pagan conjuntamente con los intereses, formando los términos amortizativos.

Según la cuantía de los términos amortizativos, podemos distinguir los siguientes casos:

• Términos amortizativos constantes.
• Términos amortizativos variables:
  – Cuota de amortización constante.
  – Términos amortizativos variables en progresión geométrica.
  – Términos amortizativos variables en progresión aritmética.

Todo ello con independencia de que los intereses se paguen con una frecuencia u otra, sean fijos o variables, pagaderos por anticipado o al final de cada período.

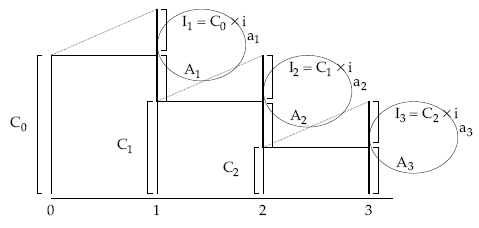
Estudiando la evolución de la deuda pendiente se observa que ésta crece en el interior de cada uno de los períodos en los que se divide la operación, para disminuir al final de los mismos como consecuencia de la entrega del término amortizativo.

Se producen, por tanto, dos movimientos de signo contrario en cada uno de los períodos: uno de crecimiento por efecto de los intereses generados y otro de disminución por el pago del término amortizativo.La suma de estos dos movimientos nos da la variación total de la deuda pendiente al final del período. Esta variación supondrá una disminución de la deuda caso de ser el término amortizativo mayor que los intereses generados en el período y supondrá un incremento de la deuda en el supuesto contrario, es decir, la cuota de interés mayor que el término amortizativo. En el caso concreto de que la cuantía del término amortizativo coincida con la cuota de interés no habrá variación de la deuda.

El gráfico de evolución de la deuda pendiente de un préstamo y los pagos realizados durante tres períodos será el siguiente:

1.2.
NOMENCLATURA PARA PRÉSTAMOS DE AMORTIZACIÓN
FRACCIONADA

La terminología utilizada será la siguiente:

C₀: Importe del préstamo, cantidad financiada.
n:
Número de pagos a realizar durante el tiempo que se mantiene contraída la deuda.
i: Tipo de interés efectivo convenido (coste de la financiación).
a_k:
Término amortizativo al final del período k, pago total realizado por el prestatario en cada vencimiento (mensual, trimestral, semestral, …).

a_k = I_k + A_k

I_k:
Cuota de interés del período k, cantidad destinada a remunerar al prestamista por el período correspondiente.
A_k:
Cuota de amortización del período k, cantidad destinada a devolver deuda en cada vencimiento.
C_k:
Capital pendiente de amortización en el momento k. También se llama capital vivo, saldo de la operación o reserva matemática.
m_k:
Capital total amortizado al final del período k.

1.3. GENERALIDADES

1. Los intereses de cada período se calculan sobre el capital vivo a principio del período.

I_k = C_k-1 x i

2. El parámetro que amortiza directamente el capital es la cuota de amortización (A), e indirectamente el término amortizativo.
3. El capital a amortizar siempre es la suma aritmética de todas las cuotas de amortización.

C₀ = A₁ + A₂ + … + A_n

4. El capital vivo (pendiente) es la suma aritmética de las cuotas de amortización que queden por amortizar.

C_k = A_k+1 + A_k+2 + … + A_n

Aunque también se obtiene por la diferencia entre el importe del préstamo y el total amortizado hasta ese momento.

C_k = C₀ – (A₁ + A₁ + … + A_k) = C₀ – m_k

Sin embargo, y a pesar de la sencillez de los sistemas anteriormente comentados, lo más frecuente consiste en fraccionar la devolución de la deuda destinando los términos amortizativos simultáneamente a pagar los intereses devengados en el período y cancelar parte de la deuda pendiente.

En estos casos resulta útil recoger en un cuadro el proceso de amortización del capital, reflejando de forma clara y concisa el valor que toman las principales variables en los diversos vencimientos de la operación.

La denominación será la de cuadro de amortización, y en él vamos a reflejar las cuantías de los términos amortizativos (a_k), las cuotas de intereses (I_k) y las cuotas de amortización (A_k) correspondientes a cada uno de los períodos, así como las cuantías del capital vivo (C_k) y del capital amortizado (m_k) referidos a cada período de la operación.

El cuadro resultante es: